CSE 2320 - Assignments

Not Graded Practice for Assignment 6

Practice Question 1

(This is Problem 5.37 from the textbook).

Write a function that computes Fibonacci(N) mod M, using only a constant amount of space for intermediate calculations.

Practice Question 2

(This is Problem 5.38 from the textbook).

What is the largest N for which Fibonacci(N) can be represented as a 64-bit integer?

Practice Question 3

(This is Problem 5.39 from the textbook).

Draw the tree corresponding to Figure 5.15 for the case where we exchange the recursive calls in Program 5.11.

Practice Question 4

(This is Problem 5.40 from the textbook).

Write a function that uses bottom-up dynamic programming to compute the value of P(N) defined by the recurrence:

P(N) = floor(N/2) + P(floor(N/2)) + P(ceiling(N/2)),         for N >= 1, with P(0) = 0.

What is the best running time complexity you can attain for this problem using bottom-up dynamic programming?

Practice Question 5

(This is Problem 5.41 from the textbook).

Write a function that uses top-down dynamic programming to solve the previous exercise.

(This part is a challenge:) What is the best running time complexity you can attain for this problem using top-down dynamic programming?

Practice Question 6

(This is Problem 5.42 from the textbook).

Draw a tree similar to that of Figure 5.15, for your function from the previous exercise (textbook exercise 5.41), when invoked for N = 23.

Practice Question 7

(This is Problem 5.43 from the textbook).

Draw a plot of N versus the number of recursive calls that your function from textbook exercise 5.41 makes to compute P(N), for 0 <= N <= 1024.(For the purposes of this calculation, start your program from scratch for each N.)

Practice Question 8

(This is Problem 5.44 from the textbook).

Write a function that uses bottom-up dynamic programming to compute the value of CN defined by the recurrence

Practice Question 9

(This is Problem 5.45 from the textbook).

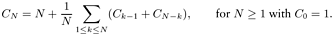
Write a function that uses top-down dynamic programming to solve the previous exercise.

Practice Question 10

(This is Problem 5.46 from the textbook).

Draw a tree similar to that of Figure 5.15, for your function from the previous exercise (textbook exercise 5.45), when invoked for N = 23.

Practice Question 11

(This is Problem 5.47 from the textbook).

Draw a plot of N versus the number of recursive calls that your function from textbook exercise 5.45 makes to compute CN, for 0 <= N <= 1024.(For the purposes of this calculation, start your program from scratch for each N.)

Back to the list of assignments.