CSE 4308/5360 - Assignments
Assignment 2 (Written 1)

Solution

Due date: Thursday, September 20, 2007, in class.

This is a written assignment. Handwritten or printed solutions will be accepted. Solutions must be submitted in class on Thursday, September 20, 2007. As usual, students registered for CSE 4308 are welcome to do the CSE 5360 portions of the assignment for extra credit. There are also two extra credit problems (problems 4 and 5) that all students are welcome to try to answer.

1). (10 points). Consider the search tree shown in Figure 1. List the order in which nodes will be visited using:
Figure 1. An example search tree.

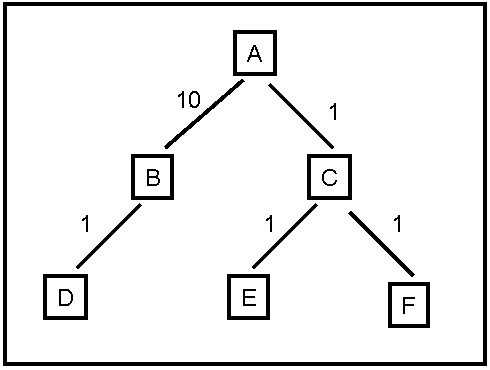
2). (CSE 4308: 20 points, CSE 5360: 30 points) A social network graph (SNG) is a graph where each vertex is a person and each edge represents an acquaintance. In other words, an SNG is a graph showing who knows who. For example, in the graph shown on Figure 2, George knows Mary and John, Mary knows Christine, Peter and George, John knows Christine, Helen and George, Christine knows Mary and John, Helen knows John, Peter knows Mary.

The degrees of separation measure how closely connected two people are in the graph. For example, John has 0 degrees of separation from himself, 1 degree of separation from Christine, 2 degrees of separation from Mary, and 3 degrees of separation from Peter.

a). (5 points) From among breadth-first search, depth-first search, iterative deepening search, and uniform cost search, which one(s) guarantee finding the correct number of degrees of separation between any two people in the graph?

b). (5 points) For the SNG shown in Figure 2, draw the first three levels of the search tree, with John as the starting point (the first level of the tree is the root). Is there a one-to-one correspondence between nodes in the search tree and vertices in the SNG? Why, or why not?

c). (5 points) Draw an SNG containing exactly 5 people, where at least two people have 4 degrees of separation between them.

d). (5 points) Draw an SNG containing exactly 5 people, where all people have 1 degree of separation between them.

e). (5 points, CSE 5360 only) Is there a non-empty SNG where all people have 2 degrees (no more, no less) of separation between them? Draw an example, or prove that there is no such SNG (the answer is very simple, if you try anything complicated you are on the wrong track).

f). (5 points, CSE 5360 only) In an implementation of breadth-first search for finding degrees of separation, suppose that every node in the search tree takes 1KB of memory. Suppose that the SNG contains one million people. Outline (briefly but precisely) how to make sure that the memory required to store search tree nodes will not exceed 1GB (the correct answer can be described in one-two lines of text).


Figure 2: A social network graph (SNG).

3). (CSE 4308: 20 points, CSE 5360: 25 points) Figures 3 and 4 show maps where all the towns are on a grid. Each town T has coordinates (Ti, Tj), where Ti Tj are non-negative integers. We use the term Euclidean distance for the straight-line distance between two towns, and the term driving distance for the length of the shortest driving route connecting two towns. The only roads that exist connect towns that have Euclidean (straight-line) distance 1 from each other (however, there may be towns with Euclidean distance 1 from each other that are NOT directly connected by a road, for example in Figure 4).

a). (10 points) On the map shown on Figure 3, every town is directly connected to all towns within Euclidean distance 1 from each other. On this map, if two towns have driving distance 4 from each other, what is the maximum possible number of nodes on the search tree that will be expanded by breadth-first search? How about depth-first search? For this question, assume that the search algorithm does not keep track of nodes already visited. Answers within 10 of the correct answer will get full points.

b). (10 points) Consider best-first search, where the node to be expanded is always the one with the shortest Euclidean distance to the destination. Also consider A* search, where h(n) is the Euclidean distance from n to the destination (remember that the next node is picked not based on h(n) but based on f(n) = g(n) + h(n)). For each of the maps showing on Figures 3 and 4, answer the following: does best-first search always perform better than A*, does best-first search always perform worse than A*, or does it depend on the start and destination towns? Why?

c). (5 points, CSE 5360 only) Define an admissible heuristic h to be used with A* (i.e., an h(n) that never gives a value higher than the shortest driving distance from n to the destination), that (for at least some cases) is more accurate than the Euclidean distance between n and the destination. Your h must be correct for the maps shown in Figures 3 and 4. It does not have to be correct on all possible maps.


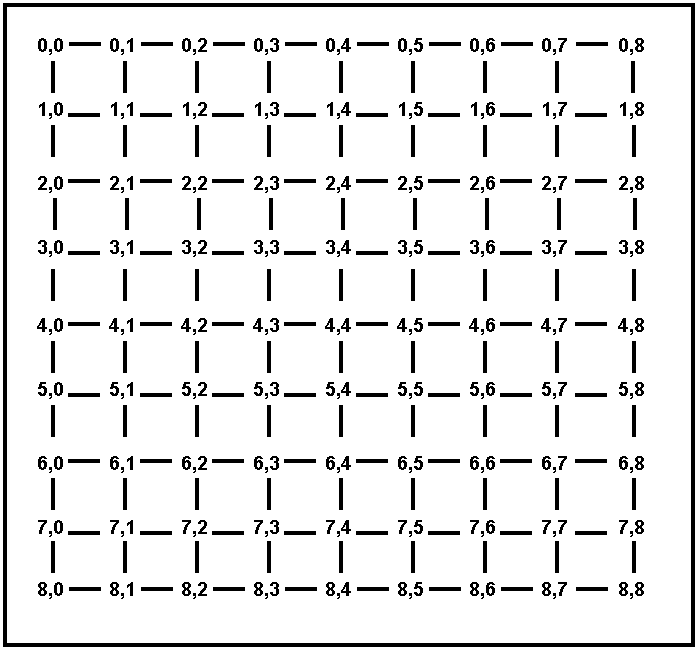
Figure 3. A map of cities on a fully connected grid. Every city is simply named by its coordinates.



Figure 4. A map of cities on a partially connected grid. Every city is simply named by its coordinates.

4. (optional extra credit, 5 points). In the context of A* search, it is actually possible to have admissible functions h1 and h2 such that: h2 dominates h1 (i.e., h1 <= h2 ), but, for at least some searches, A* visits fewer nodes using h1 than using h2 . Illustrate such an example (draw the search tree, and define functions h1 and h2 , and show the nodes visited for each of the functions).
5. (optional extra credit, 5 points). Give an example (i.e., describe a search tree) where A* gets stuck in an infinite loop, and fails to find an optimal solution.