CSE 4308/5360 - Assignments
CSE 4308 Assessment / CSE 5360 Assignment 6

Due dates for CSE 4308 (assessment):
For CSE 5360 Only: All parts due Tuesday, December 4, 11:59pm (by e-mail).

Summary

The goal of this assignment/assessment is to evaluate theoretical understanding of Bayesian networks and the practical ability to design and implement such networks. Four tasks need to be completed:
  1. Answering some written questions about Bayesian networks.
  2. Designing a Bayesian network graph given a description of the problem in English.
  3. Using training data to learn probability distributions for a Bayesian network.
  4. Implementing a Bayesian network in software. Your implementation must be able to compute the probability of any event.

Part 1 (Theoretical Understanding): Questions about Bayesian Networks.

Questions 1-6 refer to the Bayesian network in Figure 1. Questions 7 and 8 refer to the Bayesian network in Figure 2.
  1. Consider the event E = "battery age is less than three years". Let A = P(E | "battery dead"=true AND "no oil"=true) and B = P(E | "battery dead"=true AND "no oil"=false). Which of the following three cases can possibly be true: A > B, A = B, or A < B? Why?
  2. Consider again the event E = "battery age is less than three years". Let A = P(E | "battery dead"=true AND "no oil"=true) and B = P(E | "battery dead"=true AND "starter broken"=true). Which of the following three cases can possibly be true: A > B, A = B, or A < B? Why?
  3. The "alternator broken" event and the "fanbelt broken" event are both causes of the "no charging event." Let A = P("alternator broken"=true | "no charging"=true) and B = P("alternator broken"=true | "no charging"=true AND "fanbelt broken"=true). Which of the following three cases do you expect to be true: A > B, A = B, or A < B? Why?
  4. The "no gas" event is a cause of the "car won't start" event. Let A = P("no gas"=true) and B = P("no gas"=true | "car won't start"=true). Which of the following three cases do you expect to be true: A > B, A = B, or A < B? Why?
  5. Suppose that: What is P("no charging"=false)? How is it derived?
  6. Suppose that: What is P("battery age" <= 3 years | "battery dead"=true)? How is it derived?
  7. In Figure 2, what is the probability of the following event: burglary=false AND earthquake=true AND alarm=false AND JohnCalls=true AND MaryCalls=false.
  8. In Figure 2, what is the probability of the following event: earthquake=true AND alarm=false AND JohnCalls=true AND MaryCalls=false.


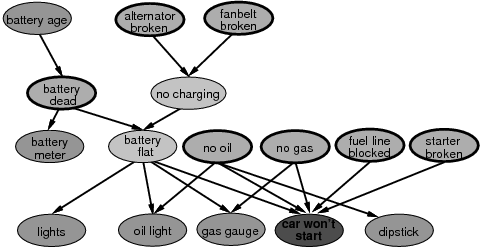
Figure 1: A Bayesian network graph establishing relations between various car problems and their causes.

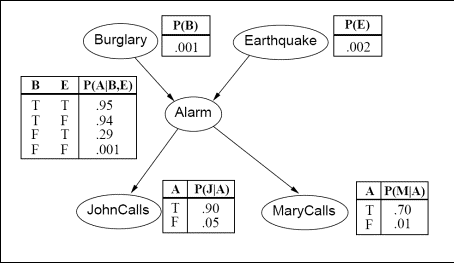
Figure 2: A Bayesian network establishing relations between events, together with complete specifications of all probability distributions.

Part 2 (Solution Design): Designing a Bayesian network graph.

George doesn't watch much TV in the evening, unless there is a baseball game on. When there is baseball on TV, George is very likely to watch. George has a cat that he feeds every night, although he forgets every now and then. He's much more likely to forget when he's watching TV. He's also very unlikely to feed the cat if he has run out of cat food (although sometimes he gives the cat some of his own food). Design a Bayesian network for modeling the relations between these four events: Your task is to connect these nodes with arrows pointing from causes to effects. No programming is needed for this part, just submit a document showing your Bayesian network design.

Part 3 (Data Analysis): Learning Probabilities from Training Data.

For the Bayesian network of Part 2, the text file at this link contains training data from every evening of an entire year. Every line in this text file corresponds to an evening, and contains four numbers. Each number is a 0 or a 1. In more detail: Based on the data in this file, determine the probability table for each node in the Bayesian network you have designed for Part 2. You need to submit these four tables by e-mail. Optionally (to help with grading) you can also submit the code that computes these probabilities.

Part 4 (Software Implementation): Implementing a Bayesian Network in Software.

For the Bayesian network of Figure 2, implement a program that computes the probability of any combination of events. For example, if the executable is called bnet, an example invocation of the executable would be: 
bnet 0 1 0 1 1
In general, bnet takes exactly 5 (no more, no fewer) command line arguments, and each argument is either 0 or 1. The arguments provide to the program the following information:
  1. The first argument is 1 if Burglary=true, and 0 if Burglary=false.
  2. The second argument is 1 if Earthquake=true, and 0 if Earthquake=false.
  3. The third argument is 1 if Alarm=true, and 0 if Alarm=false.
  4. The fourth argument is 1 if JohnCalls=true, and 0 if JohnCalls=false.
  5. The fifth argument is 1 if MaryCalls=true, and 0 if MaryCalls=false.
The correct implementation will not contain hardcoded values for all 32 combinations of arguments, but instead will use the tables shown on Figure 2 and the appropriate formulas to evaluate the probability of the specified event.

Grading Rubric

Each of the four parts is worth 25 points. For the assessment, in addition to the points, there will also be a qualitative grade for each part, and for the assessment as a whole. The qualitative grade can have the following five values: poor, fair, acceptable, goods, excellent. The qualitative grade will be assigned as follows: Here is additional information about how each part will be graded:

Submissions

All submissions are via e-mail. E-mail your submission to BOTH the instructor and the TA. Use subject "CSE 4308 assessment, part X" or "CSE 5360, assignment 6, part X". where X is the part of the assignment that you are submitting.

For part 4, implementations in LISP, C, C++, and Java will be accepted. If you would like to use another language, please first check with the instructor via e-mail.

For part 4, submit a zipped directory (no other forms of compression accepted) via e-mail, with subject "CSE 4308/5360, assignment 6". THE ATTACHMENT SHOULD NOT EXCEED 800KB in size (e-mail the instructor if the 800KB limit is a concern). The directory should contain source code, and optionally, binaries that are appropriate for gamma or omega. The directory should also contain a file called readme.txt, which should specify precisely:

Insufficient or unclear instructions will be penalized severely. Code that does not run on at least one of the gamma and omega machines gets zero points.

Some hints