CSE 4308/5360 - Assignments - Written Assignment 1

Due date: Thursday 09/18/2008, in class.

Handwritten or printed solutions will be accepted. Solutions must be submitted in class on Thursday, September 18, 2008, or by e-mail, BEFORE the beginning of class on Thursday, September 18.

1). (25 points). Consider the search tree shown in Figure 1. The number next to each edge is the cost of the performing the action corresponding to that edge. List the order in which nodes will be visited using:
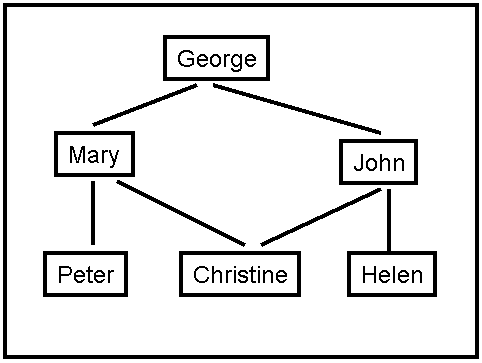
Figure 1. An example search tree.

2). A social network graph (SNG) is a graph where each vertex is a person and each edge represents an acquaintance. In other words, an SNG is a graph showing who knows who. For example, in the graph shown on Figure 2, George knows Mary and John, Mary knows Christine, Peter and George, John knows Christine, Helen and George, Christine knows Mary and John, Helen knows John, Peter knows Mary.

The degrees of separation measure how closely connected two people are in the graph. For example, John has 0 degrees of separation from himself, 1 degree of separation from Christine, 2 degrees of separation from Mary, and 3 degrees of separation from Peter.

a). (10 points) From among breadth-first search, depth-first search, iterative deepening search, and uniform cost search, which one(s) guarantee finding the correct number of degrees of separation between any two people in the graph?

b). (10 points) For the SNG shown in Figure 2, draw the first three levels of the search tree, with John as the starting point (the first level of the tree is the root). Is there a one-to-one correspondence between nodes in the search tree and vertices in the SNG? Why, or why not? In your answer here, you should assume that the search algorithm does not try to avoid revisiting the same state.

c). (10 points) Draw an SNG containing exactly 5 people, where at least two people have 4 degrees of separation between them.

d). (10 points) Draw an SNG containing exactly 5 people, where all people have 1 degree of separation between them.

e). (10 points) In an implementation of breadth-first search for finding degrees of separation, suppose that every node in the search tree takes 1KB of memory. Suppose that the SNG contains one million people. Outline (briefly but precisely) how to make sure that the memory required to store search tree nodes will not exceed 1GB (the correct answer can be described in one-two lines of text). In your answer here you are free to enhance/modify the breadth-first search implementation as you wish, as long as it remains breadth-first (a modification that, for example, converts breadth-first search into depth-first search or iterative deepening search is not allowed).


Figure 2: A social network graph (SNG).

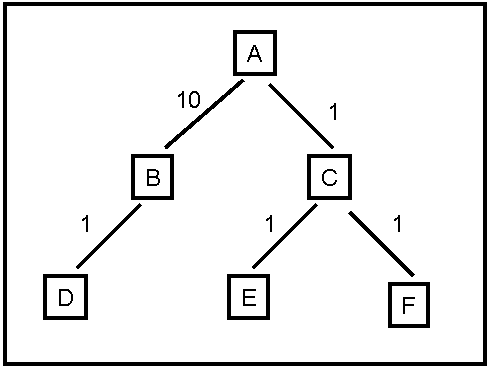
3). (25 points) Figures 3 and 4 show maps where all the towns are on a grid. Each town T has coordinates (Ti, Tj), where Ti Tj are non-negative integers. We use the term Euclidean distance for the straight-line distance between two towns, and the term driving distance for the length of the shortest driving route connecting two towns. The only roads that exist connect towns that have Euclidean (straight-line) distance 1 from each other (however, there may be towns with Euclidean distance 1 from each other that are NOT directly connected by a road, for example in Figure 4).

Consider best-first search, where the node to be expanded is always the one with the shortest Euclidean distance to the destination. Also consider A* search, where h(n) is the Euclidean distance from n to the destination (remember that the next node is picked not based on h(n) but based on f(n) = g(n) + h(n)). For each of the maps showing on Figures 3 and 4, answer the following: does best-first search always perform better than A*, does best-first search always perform worse than A*, or does it depend on the start and destination towns? Why? For the purposes of this question, the performance of a search algorithm is simply measured by the number of nodes visited by that algorithm.


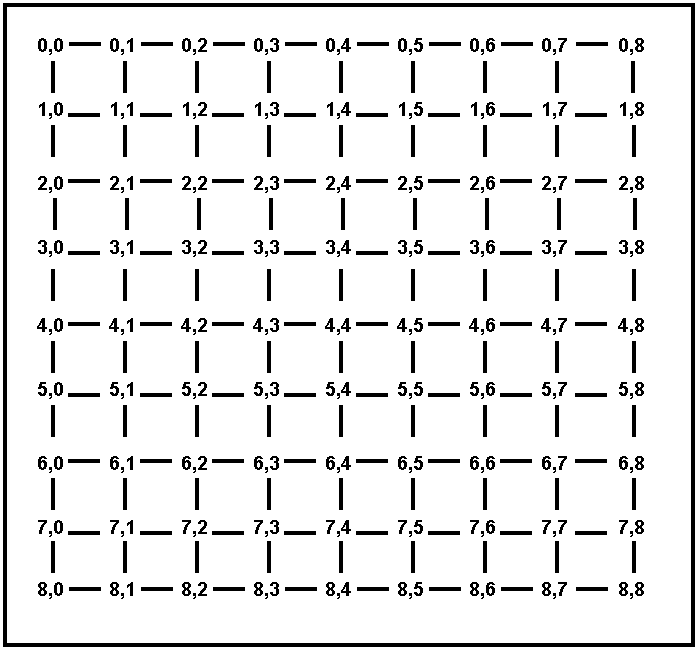
Figure 3. A map of cities on a fully connected grid. Every city is simply named by its coordinates.



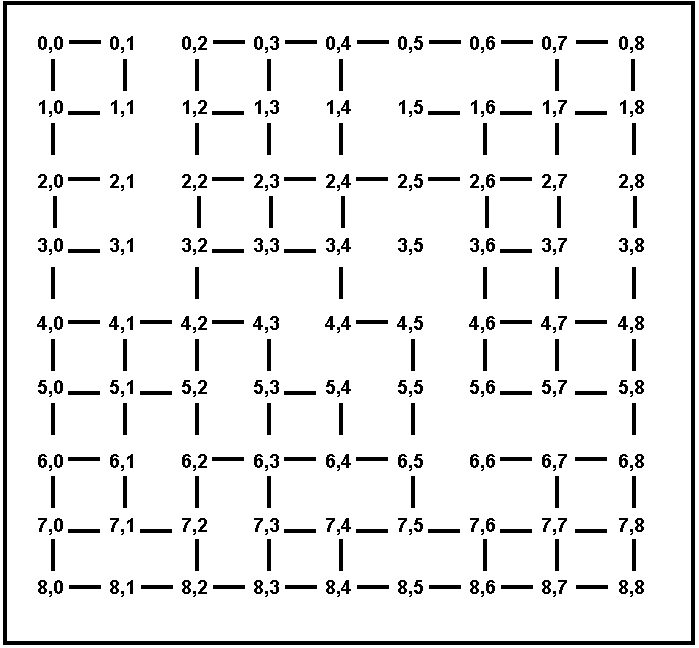
Figure 4. A map of cities on a partially connected grid. Every city is simply named by its coordinates.