Samples for Exam 2

Task 1

Figure 1: A game search tree.

a. In the game search tree of Figure 1, if we use Minmax algorithm to find the strategy to use, indicate the minmax values are for all the nodes. Also incidcate which action the Minmax algorithm will pick to exectute.

b. In the game search tree of Figure 1, indicate what nodes will be pruned using alpha-beta search, and what the minmax values are for the rest of the nodes. Assume that alpha-beta search expands nodes in a left-to-right order. Finally incidcate which action the Minmax algorithm will pick to exectute. Is this answer different from part a?

c. This question is also on the game search tree of Figure 1. Suppose we are given some additional knowledge about the game: the maximum utility value is 12 i.e., it is not mathematically possible for the MAX player to get an outcome greater than 12 and the minimum utility value is 2 i.e., it is not mathematically possible for the MIN player to get an outcome lower than 2. How can this knowledge be used to further improve the efficiency of alpha-beta search? Indicate the nodes that will be pruned using this improvement. Again, assume that alpha-beta search expands nodes in a left-to-right order.

Task 2

Suppose that you want to implement an algorithm that will compete on a two-player deterministic game of perfect information. Your opponent is a supercomputer called DeepGreen. DeepGreen does not use Minimax. You are given a library function DeepGreenMove(S), that takes any state S as an argument, and returns the move that DeepGreen will choose for that state S (more precisely, DeepGreenMove (S) returns the state resulting from the opponent's move).

Write an algorithm in pseudocode (following the style of the Minimax pseudocode) that will always make an optimal decision given the knowledge we have about DeepGreen. You are free to use the library function DeepGreenMove(S) in your pseudocode. What advantage would this algorithm have over Minimax? (if none, Justify).

Task 3 [Note: Only included in Final for Sections 001, 003 and 005. Included in Exam 2 and Final for Sections 002 and 004]

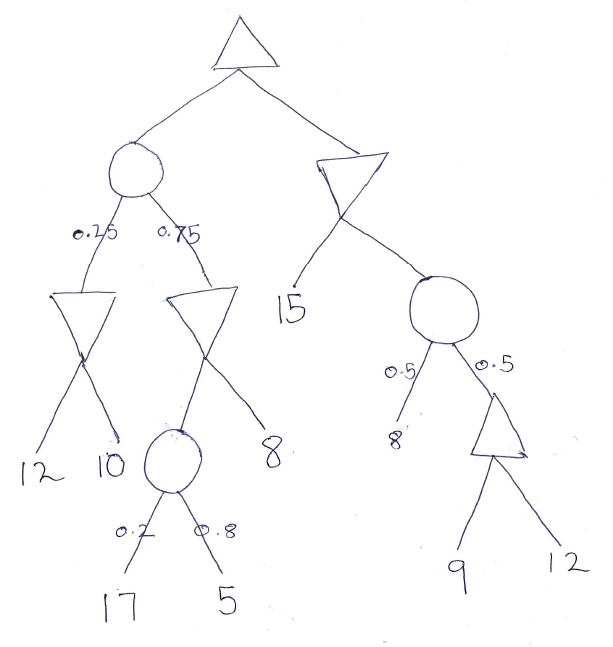
Figure 2: An Expectiminmax tree.

Find the value of every non-terminal node in the expectiminmax tree given above. Also indicate which action will be performed by the algoirithm. What is lowest and highest possible outcome of a single game if the minmax strategy is followed against an optimal opponent?

Task 4

Consider the following map.

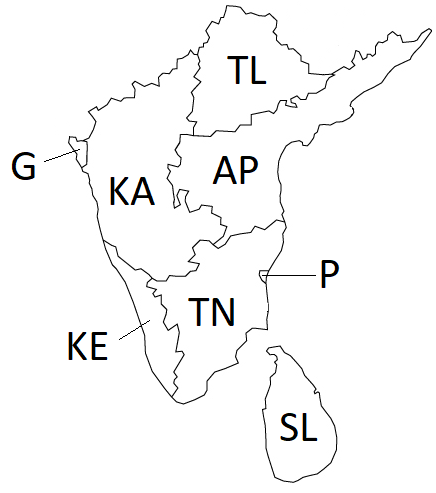
Figure 3: Outline of a Map

The problem is to color the sections such that no two sections sharing a border have the same color. You are allowed to use the colors (Red, Green, Blue).

Part a: Draw the Constraint Graph for this problem.

Part b: Assuming you are using Backtracking search to solve this problem and that you are using MRV with Degree heuristic to select the variable, Which variable will be selected at each level of the search tree [You do not need to draw the tree. Just let me know which variable will be selected and why (MRV and degree values)]. Note: Multiple possible correct answers. You only have to give one.

Part c: Assume you assign the color 'Red' to the first variable selected in part b. Show the steps involved in checking the remaining legal values for all other variables using Arc Consistency.

Part d: Can you use structure of the problem to make solving it more efficient?

Part e: Give one valid solution to this problem. (You just have to give the solution. No need to give all the steps)

Task 5

A	B	C	KB	S1
True	True	True	True	True
True	True	False	False	True
True	False	True	True	True
True	False	False	False	True
False	True	True	False	False
False	True	False	False	False
False	False	True	True	True
False	False	False	False	False

KB and S1 are two propositional logic statements, that are constructed using symbols A, B, C, and using various connectives. The above truth table shows, for each combination of values of A, B, C, whether KB and S1 are true or false.

Part a: Given the above information, does KB entail S1? Justify your answer.

Part b: Given the above information, does statement NOT(KB) entail statement NOT(S1)? Justify your answer.

Task 6

Suppose that some knowledge base contains various propositional-logic sentences that utilize symbols A, B, C, D (connected with various connectives). There are only two cases when the knowledge base is false:
- First case: when A is true, B is false, C is true, D is false.
- Second case: when A is false, B is false, C is true, D is true.

In all other cases, the knowledge base is true. Write a conjunctive normal form (CNF) for the knowledge base.

Task 7

Consider the KB

(A => C) AND (B <=> C) AND (D => A) AND E AND [(B AND E) => G] AND (B => F) AND [(H AND I)=>D] AND (E => I) AND H

Show that this entails G (if possible) by

i. Forward Chaining
ii. Backward Chaining
iii. Resolution

Task 8

John and Mary sign the following contract:

- If it rains on Monday, then John must give Mary a check for $100 on Tuesday
- If John gives Mary a check for $100 on Tuesday, Mary must mow the lawn on Wednesday.

What truly happened those days is the following:
- It did not rain on Monday
- John gave Mary a check for $100 on Tueday
- Mary mowed the lawn on Wednesday.

Part a: Write a first order logic statement to express the contract. Make sure that you clearly define what constants and predicates that you use are. (NOTE: DO NOT use functions)

Part b: Write a logical statement to express what truly happened. When possible, use the same predicates and constants as in question 6a. If you need to define any new predicates or constants, clearly define what they stand for.

Part c: Define the symbols required to convert any KB involved in the above domanin from FOL to Propositional logic. Use this to convert the answers to part a and b to Propositional Logic.

Part d: Was the contract violated or not, Justify your answer [Note: Contract is definitely not violated if the events entail the contract. Contract is definitly violated if the events entail the opposite of the contract. Unknown otherwise]

Task 9

Does a unifier exist for these pairs of predicates. If they do, give the unifier

i. Taller(x, John); Taller(Bob, y)
ii. Taller(y, Mother(x)); Taller(Bob, Mother(Bob))
iii. Taller(Sam, Mary); Shorter(x, Sam)
iv. Shorter(x, Bob); Shorter(y, z)
v. Shorter(Bob, John); Shorter(x, Mary)

Task 10

Apply resolution to these pair of clauses if possible.

i. (NOT A(m)) OR B(x);   A(x) OR C(x)
ii. B(x) OR (NOT C(m)) OR D(m);   C(x) OR D(n)
iii. B(m) OR D(m);   C(n) OR (NOT D(n))