Samples for Exam 3

Task 1

Consider the 8-Puzzle problem. There are 8 tiles on a 3 by 3 grid. Your task is to get from some given configuration to a goal configuration. You can move a tile to an adjacent location as long as that location is empty.

Sample Initial configuration:
2
 3
 6
1
7
4
 8
 5

Sample Goal configuration:
1
 2
 3
4
 5
 6
7
 8

Your task is to define this problem in PDDL Describe the initial state and the goal test using PDDL. Define appropriate actions for this planning problem, in the PDDL language. For each action, provide a name, arguments, preconditions, and effects.

Task 2

Suppose that we are using PDDL to describe facts and actions in a certain world called JUNGLE. In the JUNGLE world there are 3 predicates, each predicate takes at most 4 arguments, and there are 5 constants. Give a reasonably tight bound on the number of unique states in the JUNGLE world. Justify your answer.

Task 3

Consider the following PDDL state description for the Blocks world problem.

On(A, B)
On(B, C)
On(C, Table)
On(D, E)
On(E, Table)
Clear(A)
Clear(D)

Consider the definition of Move(block, from, to) as given in the slides

Can you perform action Move(A, B, D) in this state.

What is the outcome of performing this action in this state.

Task 4

Consider the given joint probabilty distribution for a domain of two variables (Color, Vehicle) :

Color = Red
 Color = Green
 Color = Blue
Vehicle = Car
 0.1184
 0.1280
 0.0736
Vehicle = Van
 0.0444
 0.0480
 0.0276
Vehicle = Truck
 0.1554
 0.1680
 0.0966
Vehicle = SUV
 0.0518
 0.0560
 0.0322

Part a: Calculate P ( Color is not Green | Vehicle is Truck )

Part b: Check if Vehicle and Color are totally independant from each other

Task 5

In a certain probability problem, we have 11 variables: A, B1, B2, ..., B10. Based on these facts:

Part a: How many numbers do you need to store in the joint distribution table of these 11 variables?

Part b: What is the most space-efficient way (in terms of how many numbers you need to store) representation for the joint probability distribution of these 11 variables? How many numbers do you need to store in your solution? Your answer should work with any variables satisfying the assumptions stated above.

Part c: Does this scenario follow the Naive-Bayes model?


Task 6

Part a (Solve before Part b)

George doesn't watch much TV in the evening, unless there is a baseball game on. When there is baseball on TV, George is very likely to watch. George has a cat that he feeds most evenings, although he forgets every now and then. He's much more likely to forget when he's watching TV. He's also very unlikely to feed the cat if he has run out of cat food (although sometimes he gives the cat some of his own food). Design a Bayesian network for modeling the relations between these four events: Your task is to connect these nodes with arrows pointing from causes to effects.

Part b (Solve after Part a)

You have been given the correct answer for Part A (here). You have also been given the conditional probabilties of each variable given it's parents. Calculate P ( not(Baseball Game on TV) | not(George Feeds Cat) ) using Inference by Enumeration

Task 7

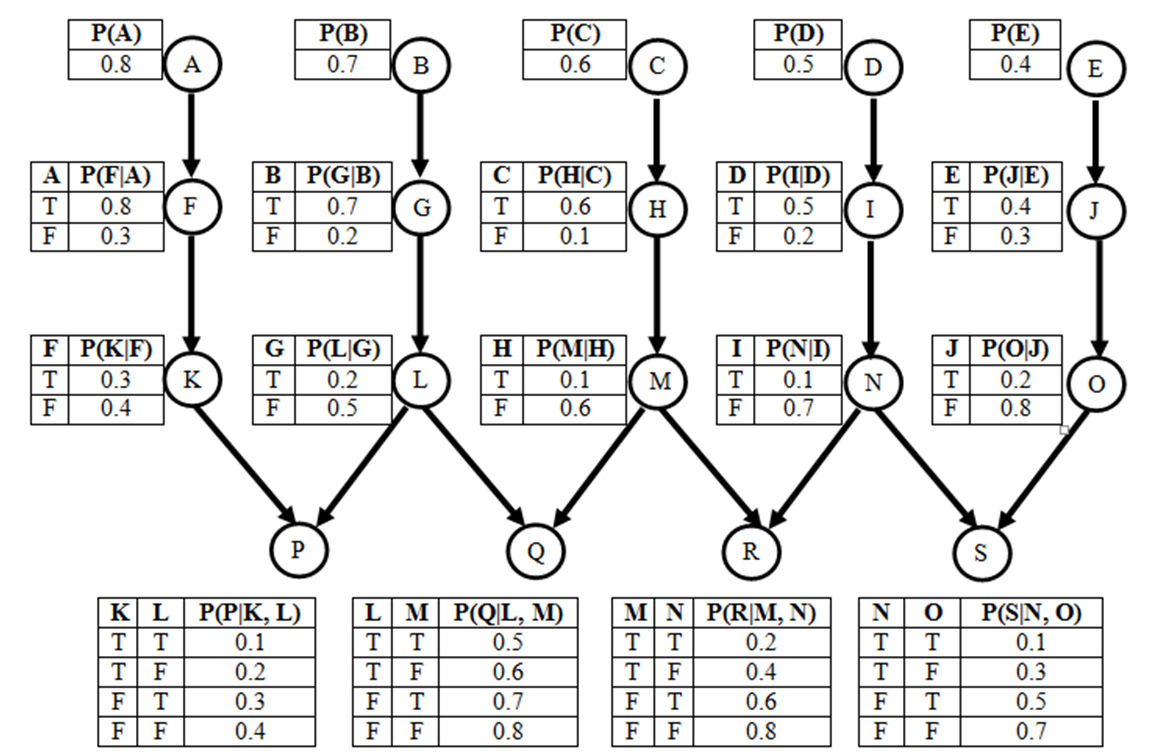
Large Bayesian Network

Part a: On the network shown above, what is the Markovian blanket of node L?

Part b: On the network shown above, what is P(A, F)? How is it derived?

Part c: On the network shown above, what is P(M, not(C) | H)? How is it derived?

Note: You do not have to use Inference by Enumeration for parts b and c.