Programming Assignment 5

Summary

The goal in this assignment is to get practice on designing Bayesian networks, estimating probability distributions in Bayesian networks, and implementing Bayesian networks.

Part 1: Posterior Probablities

30 points
 The task in this part is to implement a system that: As in the slides that we saw in class, there are five types of bags of candies. Each bag has an infinite amount of candies. We have one of those bags, and we are picking candies out of it. We don't know what type of bag we have, so we want to figure out the probability of each type based on the candies that we have picked.

The five possible hypotheses for our bag are:

Command Line arguments:

The program takes a single command line argument, which is a string, for example CLLCCCLLL. This string represents a sequence of observations, i.e., a sequence of candies that we have already picked. Each character is C if we picked a cherry candy, and L if we picked a lime candy. Assuming that characters in the string are numbered starting with 1, the i-th character of the string corresponds to the i-th observation. The program should be invoked from the commandline as follows: 
compute_a_posteriori observations
For example: 
compute_a_posteriori CLLCCLLLCCL
We also allow the case of not having a command line argument at all, this represents the case where we have made no observations yet.

Output:

Your program should create a text file called "result.txt", that is formatted exactly as shown below. ??? is used where your program should print values that depend on its command line argument. Five decimal points should appear for any floating point number. 
Observation sequence Q: ???
Length of Q: ???

P(h1 | Q) = ???
P(h2 | Q) = ???
P(h3 | Q) = ???
P(h4 | Q) = ???
P(h5 | Q) = ???

Probability that the next candy we pick will be C, given Q: ???
Probability that the next candy we pick will be L, given Q: ???

Part 2: Designing a Bayesian network graph

10 points

George doesn't watch much TV in the evening, unless there is a baseball game on. When there is baseball on TV, George is very likely to watch. George has a cat that he feeds most evenings, although he forgets every now and then. He's much more likely to forget when he's watching TV. He's also very unlikely to feed the cat if he has run out of cat food (although sometimes he gives the cat some of his own food). Design a Bayesian network for modeling the relations between these four events:

Your task is to connect these nodes with arrows pointing from causes to effects. No programming is needed for this part, just include an electronic document (PDF, Word file, or OpenOffice document) showing your Bayesian network design.

Part 3: Learning Probabilities from Training Data

20 points

For the Bayesian network of Part 1, the text file at this link contains training data from every evening of an entire year. Every line in this text file corresponds to an evening, and contains four numbers. Each number is a 0 or a 1. In more detail:

Based on the data in this file, determine the probability table for each node in the Bayesian network you have designed for Part 1. You need to include these four tables in the drawing that you produce for question 1. You also need to submit the code/script that computes these probabilities.

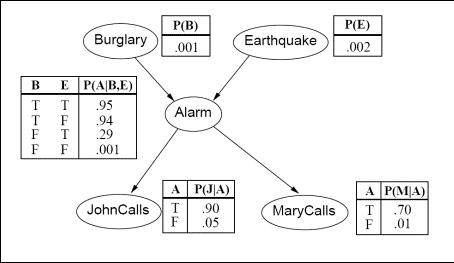
Figure 1: A Bayesian network establishing relations between events on the burglary-earthquake-alarm domain, together with complete specifications of all probability distributions.

Part 4: Implementing a Bayesian Network

40 points

For the Bayesian network of Figure 1, implement a program that computes and prints out the probability of any combination of events given any other combination of events. If the executable is called bnet, here are some example invocations of the program:

  1. To print out the probability P(Burglary=true and Alarm=false | MaryCalls=false). 
    bnet Bt Af given Mf
  2. To print out the probability P(Alarm=false and Earthquake=true). 
    bnet Af Et
  3. To print out the probability P(JohnCalls=true and Alarm=false | Burglary=true and Earthquake=false). 
    bnet Jt Af given Bt Ef
  4. To print out the probability P(Burglary=true and Alarm=false and MaryCalls=false and JohnCalls=true and Earthquake=true). 
    bnet Bt Af Mf Jt Et
In general, bnet takes 1 to 6(no more, no fewer) command line arguments, as follows: The implementation should not contain hardcoded values for all combinations of arguments. Instead, your code should use the tables shown on Figure 1 and the appropriate formulas to evaluate the probability of the specified event. It is OK to hardcode values from the tables on Figure 1 in your code, but it is not OK to hard code values for all possible command arguments, or probability values for all possible atomic events. More specifically, for full credit, the code should include and use a Bayesian network class. The class should include a member function called computeProbability(b, e, a, j, m), where each argument is a boolean, specifying if the corresponding event (burglary, earthquake, alarm, john-calls, mary-calls) is true or false. This function should return the joint probability of the five events.

Grading

Each part will be graded as follows:

How to submit

Submissions should be made using Blackboard.

Submit a ZIPPED directory called programming5.zip (no other forms of compression accepted, contact the instructor or TA if you do not know how to produce .zip files). The directory should contain source code, the answer for part 1 in a document, the answer (and code) for part 2, and the code for part 3. The submission should also contain a file called readme.txt, which should specify precisely:

Insufficient or unclear instructions will be penalized by up to 20 points. Code that does not run on omega machines gets AT MOST half credit (50 points).

Submission checklist