Written Assignment 1

The assignment should be submitted via Blackboard.

Question 1

Max: 20 Points

Consider the search tree shown in Figure 1. The number next to each edge is the cost of the performing the action corresponding to that edge. List the order in which nodes will be visited using:
Figure 1: Search Tree
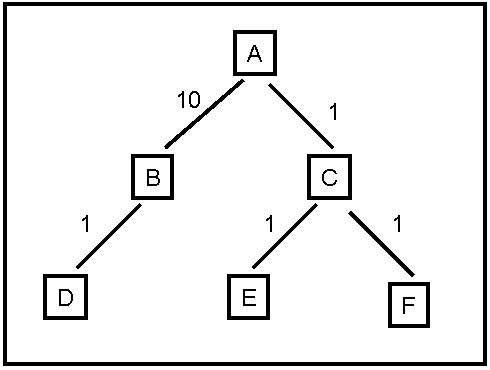
Figure 1: Search Tree for Problem 1

Question 2

Max: 30 Points

A social network graph (SNG) is a graph where each vertex is a person and each edge represents an acquaintance. In other words, an SNG is a graph showing who knows who. For example, in the graph shown on Figure 2, George knows Mary and John, Mary knows Christine, Peter and George, John knows Christine, Helen and George, Christine knows Mary and John, Helen knows John, Peter knows Mary.
The degrees of separation measure how closely connected two people are in the graph. For example, John has 0 degrees of separation from himself, 1 degree of separation from Christine, 2 degrees of separation from Mary, and 3 degrees of separation from Peter.
  1. From among breadth-first search, depth-first search, iterative deepening search, and uniform cost search, which one(s) guarantee finding the correct number of degrees of separation between any two people in the graph? (6 Points)

  2. For the SNG shown in Figure 2, draw the first three levels of the search tree, with John as the starting point (the first level of the tree is the root). Is there a one-to-one correspondence between nodes in the search tree and vertices in the SNG? Why, or why not? In your answer here, you should assume that the search algorithm does not try to avoid revisiting the same state. (6 Points)

  3. Draw an SNG containing exactly 5 people, where at least two people have 4 degrees of separation between them. (6 Points)

  4. Draw an SNG containing exactly 5 people, where all people have 1 degree of separation between them. (6 points)

  5. In an implementation of breadth-first search for finding degrees of separation, suppose that every node in the search tree takes 1KB of memory. Suppose that the SNG contains one million people. Outline (briefly but precisely) how to make sure that the memory required to store search tree nodes will not exceed 1GB (the correct answer can be described in one-two lines of text). In your answer here you are free to enhance/modify the breadth-first search implementation as you wish, as long as it remains breadth-first (a modification that, for example, converts breadth-first search into depth-first search or iterative deepening search is not allowed). (6 Points)
Figure 2: A Social Network Graph
Figure 2: A Social Network Graph

Question 3

Max: 15 Points

Figures 3 and 4 show maps where all the towns are on a grid. Each town T has coordinates (Ti, Tj), where Ti Tj are non-negative integers. We use the term Euclidean distance for the straight-line distance between two towns, and the term driving distance for the length of the shortest driving route connecting two towns. The only roads that exist connect towns that have Euclidean (straight-line) distance 1 from each other (however, there may be towns with Euclidean distance 1 from each other that are NOT directly connected by a road, for example in Figure 4).

Consider greedy search, where the node to be expanded is always the one with the shortest Euclidean distance to the destination. Also consider A* search, where h(n) is the Euclidean distance from n to the destination (remember that the next node is picked not based on h(n) but based on f(n) = g(n) + h(n)). For each of the maps showing on Figures 3 and 4, which of the following statements is true?
Justify your answer. For the purposes of this question, the performance of a search algorithm is simply measured by the number of nodes visited by that algorithm. Note that you have to provide separate answers for Figure 3 and for Figure 4.

Figure 3: Fully connected city grid
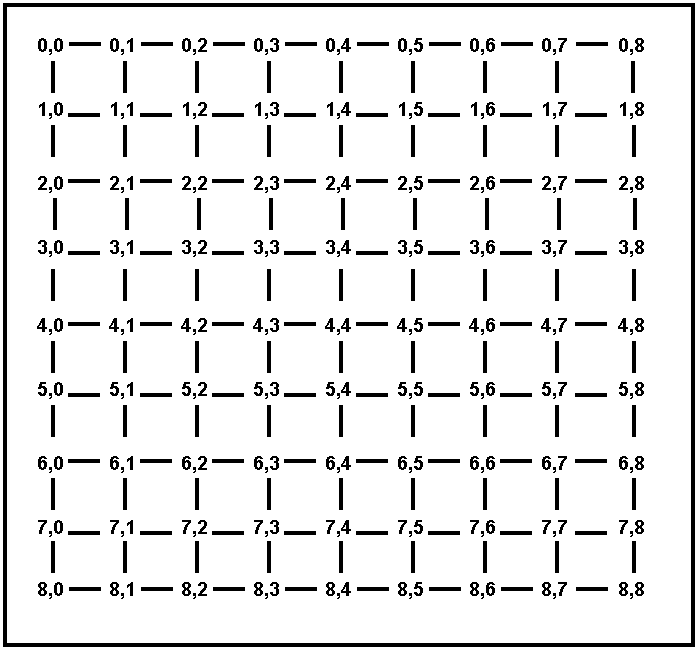
Figure 3. A map of cities on a fully connected grid. Every city is simply named by its coordinates.

Figure 4: Partialy connected city grid
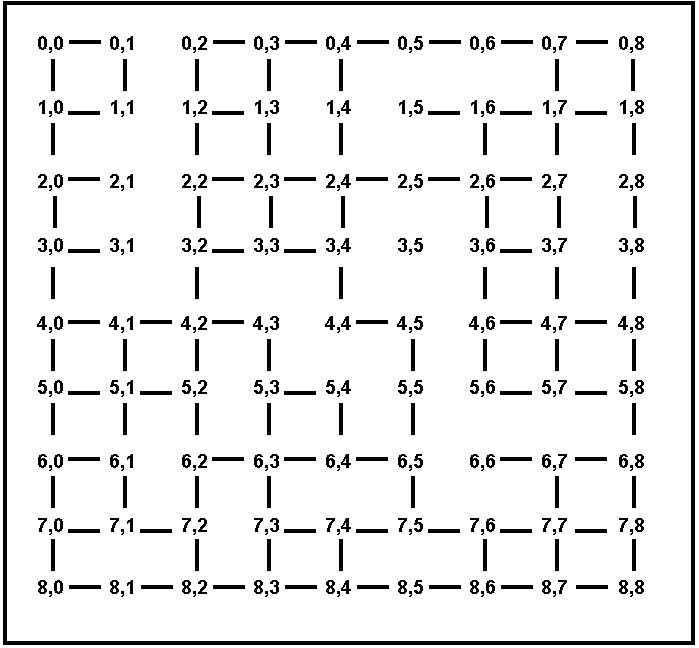
Figure 4. A map of cities on a partially connected grid. Every city is simply named by its coordinates.

Question 4

Max: 20 Points

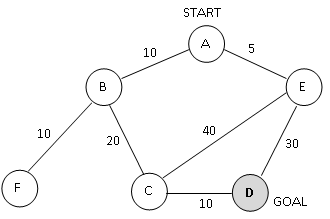Figure 5. A search graph showing states and costs of moving from one state to another. Costs are undirected.
Figure 5. A search graph showing states and costs of moving from one state to another. Costs are undirected.

Consider the search space shown in Figure 5. D is the only goal state. Costs are undirected. For each of the following heuristics, determine if it is admissible or not. For non-admissible heuristics, modify their values as needed to make them admissible.

Heuristic 1:
      h(A) = 5
      h(B) = 30
      h(C) = 20
      h(D) = 0
      h(E) = 10
      h(F) = 0

Heuristic 2:
      h(A) = 15
      h(B) = 5
      h(C) = 10
      h(D) = 0
      h(E) = 0
      h(F) = 0

Heuristic 3:
      h(A) = 35
      h(B) = 30
      h(C) = 20
      h(D) = 0
      h(E) = 0
      h(F) = 50

Heuristic 4:
      h(A) = 8
      h(B) = 5
      h(C) = 3
      h(D) = 5
      h(E) = 5
      h(F) = 0

Question 5

Max: 15 Points

Consider a search space, where each state can be red, green, blue, yellow, or black. Multiple states may have the same color. The goal is to reach any black state. Here are some rules on the successors of different states, based on their color:

Define the best admissible heuristic H that you can, using the above information. H should assign a value to a node based on the color of that node's state.
H(red) = 

H(green) = 

H(blue) = 

H(yellow) = 

H(black) =

Question 6 (Extra Credit)

Max: 15 Points

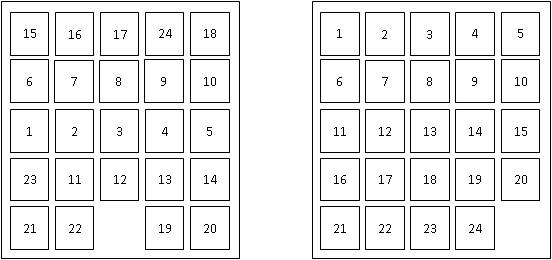Figure 6. An example of a start state (left) and the goal state (right) for the 24-puzzle.
Figure 6. An example of a start state (left) and the goal state (right) for the 24-puzzle.

The 24-puzzle is an extension of the 8-puzzle, where there are 24 pieces, labeled with the numbers from 1 to 24, placed on a 5x5 grid. At each move, a tile can move up, down, left, or right, but only if the destination location is currently empty. For example, in the start state shown above, there are three legal moves: the 12 can move down, the 22 can move left, or the 19 can move right. The goal is to achieve the goal state shown above. The cost of a solution is the number of moves it takes to achieve that solution.

For some initial states, the shortest solution is longer than 100 moves. 
For all initial states, the shortest solution is at most 208 moves.

An additional constraint is that, in any implementation, storing a search node takes 1000 bytes, i.e., 1KB of memory.

Consider breadth-first search, depth-first search, iterative deepening search, uniform cost search, A*, and IDA*.

(a): Which (if any), among those methods, can guarantee that you will never need more than 50KB of memory to store search nodes? Briefly justify your answer.

(b): Which (if any), among those methods, can guarantee that you will never need more than 1200KB of memory to store search nodes? Briefly justify your answer.

(c): Which method would you recommend as providing all these features together?

Briefly justify your answer.

Other Instructions