Written Assignment 5

The assignment should be submitted via Blackboard.

Problem 1 

30 points

You are a meteorologist that places temperature sensors all of the world, and you set them up so that they automatically e-mail you, each day, the high temperature for that day. Unfortunately, you have forgotten whether you placed a certain sensor S in Maine or in the Sahara desert (but you are sure you placed it in one of those two places) . The probability that you placed sensor S in Maine is 5%. The probability of getting a daily high temperature of 80 degrees or more is 20% in Maine and 90% in Sahara. Assume that probability of a daily high for any day is conditionally independent of the daily high for the previous day, given the location of the sensor.

Part a: If the first e-mail you got from sensor S indicates a daily high under 80 degrees, what is the probability that the sensor is placed in Maine?

Part b: If the first e-mail you got from sensor S indicates a daily high under 80 degrees, what is the probability that the second e-mail also indicates a daily high under 80 degrees?

Part c: What is the probability that the first three e-mails all indicate daily highs under 80 degrees?



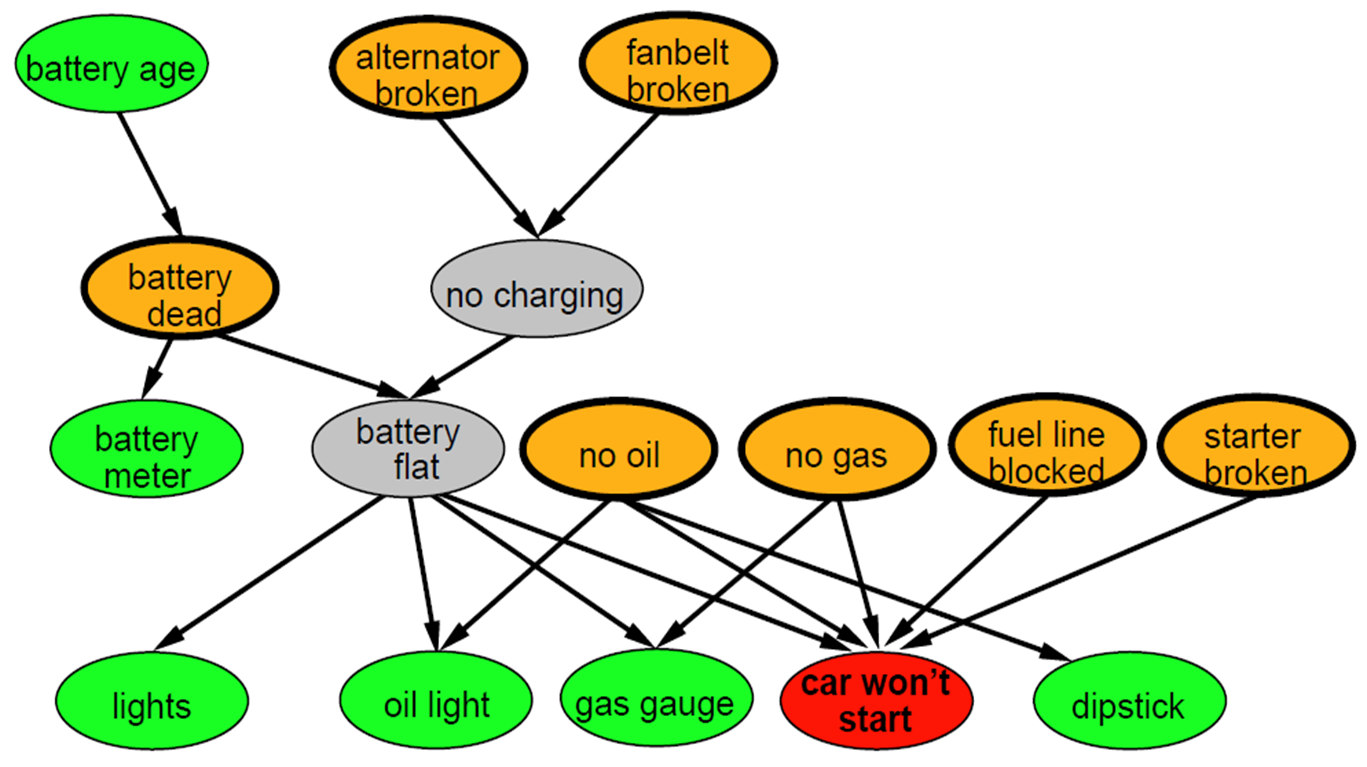
BayesianGraph

Figure 1: A Bayesian network graph establishing relations between various car problems and their causes.

Problem 2

10 points.

Suppose that:

What is P("no charging"=false)? How is it derived?

Problem 3

10 points.

On the network shown in Figure 1, suppose that:

What is P("battery age" <= 3 years | "battery dead"=true)? How is it derived?



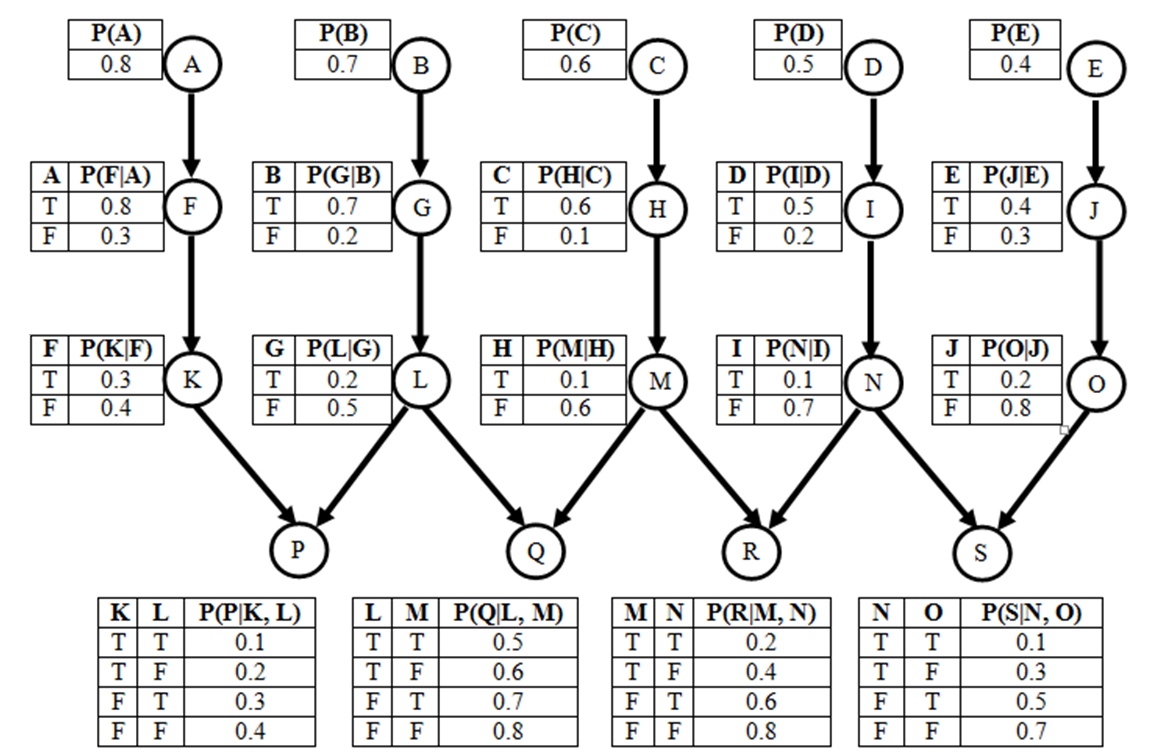
BayesianNetwork2

Figure 2: Yet another Bayesian Network.

Problem 4

30 points.

Part a: On the network shown in Figure 2, what is the Markovian blanket of node L?

Part b: On the network shown in Figure 2, what is P(A, F)? How is it derived?

Part d: On the network shown in Figure 2, what is P(M, not(C) | H)? How is it derived?

Problem 5

20 points.

In a certain probability problem, we have 11 variables: A, B1, B2, ..., B10. Based on these facts:

Part a: How many numbers do you need to store in the joint distribution table of these 11 variables?

Part b: What is the most space-efficient way (in terms of how many numbers you need to store) representation for the joint probability distribution of these 11 variables? How many numbers do you need to store in your solution? Your answer should work with any variables satisfying the assumptions stated above.

Other Instructions