Preparation for Third Midterm - Answers

Answers

- Is the following function P a valid probability function? If you answer "no", explain why not.
```
P(day == Monday) = 0.4
P(day == Tuesday) = 0.4
P(day == Wednesday) = 0.2
```
  Answer:
  Yes.
- Is the following function P a valid probability function? If you answer "no", explain why not.
```
P(day == Monday) = 0.4
P(day == Tuesday) = 0.4
P(day == Wednesday) = 0.2
P(day == Thursday) = 0.1
```
  Answer:
  No, because the sum of probabilities is 1.1, it should be 1.
- Is the following function P a valid probability density function? If you answer "no", explain why not.
```
P(x) = 0.1, if 10 <= x <= 20.
P(x) = 0 otherwise.
```
  Answer:
  Yes.
- Is the following function P a valid probability density function? If you answer "no", explain why not.
```
P(x) = 0.01, if 10 <= x <= 20.
P(x) = 0 otherwise.
```
  Answer:
  No, because the integral of P from -infinity to + infinity is 0.1, it should be 1.

Compute P(fire | alarm), given the following information:

P(alarm | fire) = A
P(alarm | not fire) = B
P(fire) = C

Answer:

P(fire | alarm) = P(alarm | fire) * P(fire) / P(alarm) = A * C / P(alarm).

P(alarm) = P(alarm, fire) + P(alarm, not fire)
= P(alarm | fire) * P(fire) + P(alarm | not fire) * P(not fire) =
= A * C + B * (1 - C)
So, if we set D = P(alarm) = A * C + B * (1 - C), our final answer is:
P(fire | alarm) = A * C / D

We are given the following information:
```
P(fire) = 0.1
P(earthquake) = 0.2
P(flood) = 0.4
```
1. Suppose that we do not know whether fire, earthquake, and flood, are independent events. Can we compute the probability P(fire and earthquake and flood)? If yes, what is P(fire and earthquake and flood)?
  Answer:
  
  No, if we do not know whether fire, earthquake, and flood, are independent events, then we would need some additional information (such as a joint distribution table) to compute P(fire and earthquake and flood).
2. Suppose that we know that fire, earthquake, and flood, are independent events. Can we compute the probability P(fire and earthquake and flood)? If yes, what is P(fire and earthquake and flood)?
  Answer:
  
  Yes.
  
  P(fire and earthquake and flood) = P(fire) * P(earthquake) * P(flood) = 0.1 * 0.2 * 0.4 = 0.008.
3. Suppose that we know that fire, earthquake, and flood, are not independent events. Can we compute the probability P(fire and earthquake and flood)? If yes, what is P(fire and earthquake and flood)?
  Answer:
  
  No, if we know that fire, earthquake, and flood are not independent events, then we would need some additional information (such as a joint distribution table) to compute P(fire and earthquake and flood).

Compute P(commute time < 20 min | temperature > 80), given the following joint probability distribution:

Commute time 40-60 Fahrenheit 60-80 Fahrenheit above 80 Fahrenheit
< 20 min 0.1 0.05 0.1 
20-40 min 0.2 0.1 0.1
> 40 min 0.05 0.1 0.2

Answer:

P(commute time < 20 min | temperature > 80) = P(commute time < 20 min AND temperature > 80) / P(temperature > 80)

P(commute time < 20 min AND temperature > 80) = 0.1

P(temperature > 80) = 0.1 + 0.1 + 0.2 = 0.4

P(commute time < 20 min | temperature > 80) = 0.1 / 0.4 = 0.25

For the Bayesian network shown in textbook figure 14.2: is P(Earthquake | Alarm) larger, equal to, or smaller than P(Earthquake | Alarm and Burglary)? You can either (not recommended) compute both probabilities, or (recommended) provide an intuitive (but correct) justification for your answer.
Answer:

We expect that P(Earthquake | Alarm) is larger than P(Earthquake | Alarm and Burglary). Burglary and Earthquake are competing causes for the Alarm event. Given that Alarm is true, if we know that one possible cause (Burglary) is true, the other competing cause (Earthquake) becomes less likely.
For the Bayesian network shown in textbook figure 14.2: is P(Earthquake | Alarm) larger, equal to, or smaller than P(Earthquake | Alarm and MaryCalls)? You can either (not recommended) compute both probabilities, or (recommended) provide an intuitive (but correct) justification for your answer.
Answer:

P(Earthquake | Alarm) is equal to P(Earthquake | Alarm and MaryCalls). Earthquake and MaryCalls are conditionally independent given the value for the Alarm event.
We are building a decision tree to determine if the next car of a person will be a regular car or a minivan. We have 100 cases as examples. The following is true for those cases:
- 40 people bought minivans. Out of those 40 people, 30 people were over 35 years of age, and 10 people were under 35 years of age.
- 60 people bought regular cars. Out of those 60 people, 12 people were over 35 years of age, and 48 people were under 35 years of age.
What is the entropy gain of selecting the "over 35 years of age" attribute as a test for the root node of the decision tree?
Answer:

We call "parent" the node with the 100 training examples, "child1" the child node that receives the examples where the age is over 35 years, and child2 the child node that receives the examples where the age is under 35. Node child1 receives 42 examples, and node child2 receives 58 examples. We denote by log2(x) the logarithm base 2 of x. Then:
```
Entropy gain = Entropy(parent) - 42/100 * Entropy(child1) - 58/100 * Entropy(child2).

Entropy(parent) = -0.4 * log2(0.4) - 0.6 * log2(0.6) = 0.971

Entropy(child1) = -(30/42) * log2(30/42) - (12/42) * log2(12/42) = 0.8631

Entropy(child2) = -(10/58) * log2(10/58) - (48/58) * log2(48/58) = 0.6632

Entropy gain = Entropy(parent) - 42/100 * Entropy(child1) - 58/100 * Entropy(child2)
= 0.971 - 0.42 * .8631 - 0.58 * 0.6632 
=> Entropy gain = 0.2238
```
Given a set of training examples, is there always a decision tree that perfectly classifies all training examples in that set? If yes, prove your answer. If no, provide a counter example.
Answer:

If there are no duplicate training examples (i.e., if no two training examples have exactly the same values for all attributes), then the answer is yes. If there are two training examples with exactly the same values for all attributes but different class labels, then the answer is no.
There are two types of candy bags, type A and type B. Both types of bags contain an infinite number of candies. A bag of type A contains 80% chocolate candies and 20% vanilla candies. A bag of type B contains 40% chocolate candies and 60% vanilla candies. The prior probability P(A) of having a bag of type A is 0.99, and the prior probability P(B) of having a bag of type B is 0.01. What is the posterior probability that we have a bag of type A if the first candy that we pick is a vanilla candy?
Answer:
```
P(A | vanilla) = P(vanilla | A) * P(A) / P(vanilla) = 0.2 * 0.99 / P(vanilla)

P(vanilla) = P(vanilla AND A) + P(vanilla AND B) 
= P(vanilla | A) * P(A) + P(vanilla | B) * P(B) 
= 0.2 * 0.99 + 0.6 * 0.01 
= 0.2040
```
Consequently:
P(A | vanilla) = P(vanilla | A) * P(A) / P(vanilla) = 0.2 * 0.99 / 0.204 = 0.9706
Design a perceptron takes two inputs X1 and X2, and that outputs +1 if X1 >= X2 + 5, and that outputs 0 if X1 < X2 + 5. Assume that the activation function returns 0 if the weighted sum of inputs is less than 0, and that the activation function returns 1 if the weighted sum of inputs is greater than or equal to 0.
Answer:
```
X1 >= X2 + 5 => X1 - X2 - 5 >= 0
```
Therefore our neuron will have the following weights:

Weight 5 for the bias input (as a reminder, the bias input is always -1).

Weight 1 for X1.

Weight -1 for X2.
Consider a function F that takes three Boolean inputs and gives a +1 response when exactly two (no more, no fewer) of those inputs are set to true (for the inputs, true is encoded by value 1, false is encoded by value 0). Can we construct a perceptron (i.e., a neuron) that models function F perfectly? Why, or why not?
Answer:

No, we cannot. Consider these two cases:
When the exact same change to an input leads (given appropriate values to the other inputs) to opposite changes in the output, then the function cannot be modeled by a neuron.
Design a neural network that implements the XOR function. You can use any number and any type of perceptrons you like. You do not have to specify the weights inside each perceptron, but you need to specify what function each perceptron implements (and, of course, the function should be a function that a perceptron can indeed model).
Answer:
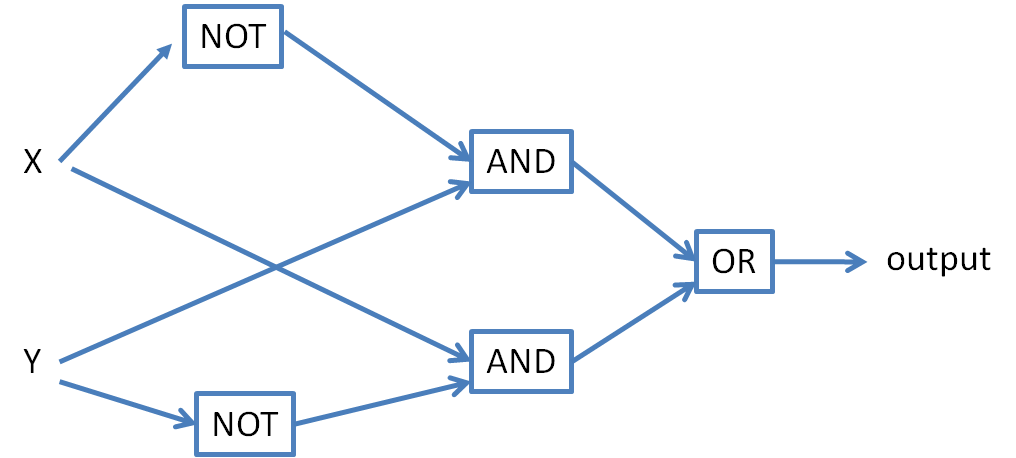
```
(X XOR Y) = ((X AND (NOT Y)) OR ((NOT X) AND Y)).
```
Consequently, using the AND, NOT, and OR neurons as defined in the textbook, the neural network for XOR looks like this: