Assignment 2
Written Assignment - Uninformed & Informed Search
Max points:
- CSE 4308: 100 (125 with EC)
- CSE 5360: 100
The assignment should be submitted via Blackboard.
Instructions
- Some questions and subsections are for CSE 5360. CSE 4308
students can answer these questions for extra credit.
- The answers can be typed as a document or handwritten and
scanned.
- Name files as
assignment2_<net-id>.<format>
- Accepted document formats are (.pdf, .doc or
.docx). If you are using OpenOffice or LibreOffice, make sure
to
save as .pdf or .doc
- Please do not submit
.txt files.
- If
you are scanning handwritten documents make sure to scan it at a
minimum of 600dpi and save as a .pdf or .png file. Do not
insert images in word document and submit.
- If there are multiple files in your submission, zip them
together as assignment2_<net-id>.zip and submit the .zip
file.
Question 1
Max: [4308: 20 Points,
5360: 16 Points]
Consider the search tree shown in Figure 1. The number next to each
edge is the cost of the performing the action corresponding to that
edge. You start from the node A. The goal is the reach node G. List the order in which nodes will be visited using:
- breadth-first search.
- depth-first search.
- iterative deepening search.
- uniform cost search.
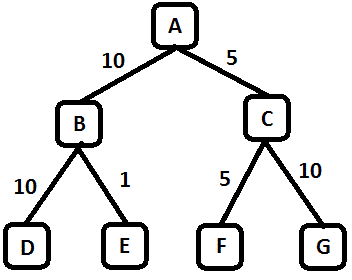
Figure 1: Search Tree for Problem 1
Question 2
Max: [4308: 30 Points,
5360: 25 Points]
A social network graph (SNG) is a graph where each vertex is a
person and each edge represents an acquaintance. In other words, an SNG
is a graph showing who knows who. For example, in the graph shown on
Figure 2, George knows Mary and John, Mary knows Christine, Peter and
George, John knows Christine, Helen and George, Christine knows Mary
and John, Helen knows John, Peter knows Mary.
The degrees of separation measure how closely connected two people are
in the graph. For example, John has 0 degrees of separation from
himself, 1 degree of separation from Christine, 2 degrees of separation
from Mary, and 3 degrees of separation from Peter.
- From among general tree search using breadth-first search,
depth-first search,
iterative deepening search, and uniform cost search, which one(s)
guarantee finding the correct number of degrees of separation between
any two people in the graph?
- For the SNG shown in Figure 2, draw the
first three
levels of the search tree, with John as the starting point (the first
level of the tree is the root). Is there a one-to-one correspondence
between nodes in the search tree and vertices in the SNG (i.e. does
every node in the search tree correspond to a vertex in the SNG)? Why,
or why
not? In your answer here, you should assume that the search algorithm
does not try to avoid revisiting the same state.
- Draw an SNG containing exactly 5 people,
where at least
two people have 4 degrees of separation between them.
- Draw an SNG containing exactly 5 people,
where all
people have 1 degree of separation between them.
- CSE 5360 Only
(5 point EC for CSE 4308): In an implementation of
breadth-first tree
search for
finding degrees of separation, suppose that every node in the search
tree takes 1KB of memory. Suppose that the SNG contains one million
people. Outline (briefly but precisely) how to make sure that the
memory required to store search tree nodes will not exceed 1GB (the
correct answer can be described in one-two lines of text). In your
answer here you are free to enhance/modify the breadth-first search
implementation as you wish, as long as it remains breadth-first (a
modification that, for example, converts breadth-first search into
depth-first search or iterative deepening search is not
allowed).
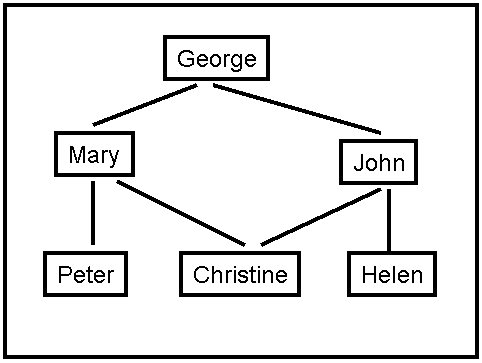
Figure 2: A Social Network Graph
Question 3
Max: [4308: 30 Points,
5360: 24 Points]
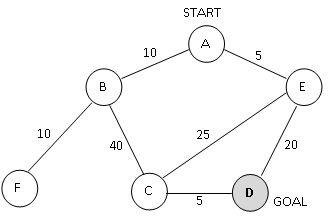 Figure
3. A search graph showing states and costs of moving from one state to
another. Costs are undirected.
Figure
3. A search graph showing states and costs of moving from one state to
another. Costs are undirected.
Consider
the search space shown in Figure 3. D is the only goal state. Costs are
undirected. For each of the following heuristics, determine if it is
admissible or not. For non-admissible heuristics, modify their values
as needed to make them admissible.
Heuristic 1:
h(A) = 5
h(B) = 40
h(C) = 10
h(D) = 0
h(E) = 10
h(F) = 0
Heuristic 2:
h(A) = 8
h(B) = 5
h(C) = 3
h(D) = 5
h(E) = 5
h(F) = 0
Heuristic 3:
h(A) = 35
h(B) = 30
h(C) = 20
h(D) = 0
h(E) = 0
h(F) = 50
Heuristic 4:
h(A) = 50
h(B) = 50
h(C) = 50
h(D) = 50
h(E) = 50
h(F) = 50
Heuristic
5:
h(A) = 0
h(B) = 0
h(C) = 0
h(D) = 0
h(E) = 0
h(F) = 0
Question 4
Max: [4308: 20 Points,
5360: 15 Points]
Consider
a search space, where each state can be a city, suburb, farmland, or
mountain. The goal is to reach any state that is a mountain. Here are some rules on the
successors of different states:
-
Successors of a city are always suburbs.
- Each city has at least one
suburb as a successor.
-
Successors of a suburb can only be cities, or suburbs, or farms.
-
Each suburb has at least one city as a successor.
-
Successors of a farm can only be farms, or suburbs, or mountains.
-
Each farm has at least one other farm as a successor.
-
Successors of a mountain can only be farms.
Define the best admissible heuristic h you can define using only the
above information (you should not assume knowledge of any additional
information about the state space). By "best admissible" we mean that
h(n) is always the highest possible value we can give, while ensuring
that heuristic h is still admissible.
You should assume that every move from one state to another has cost
1.
Question 5 (Extra Credit for 4308, Required for 5360)
Max: [4308: 20 Points EC,
5360: 20 Points]
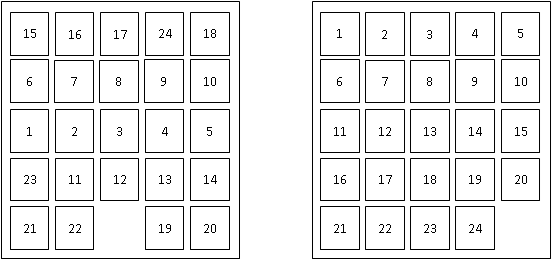 Figure
4. An example of a start state (left) and the goal state (right) for
the 24-puzzle.
Figure
4. An example of a start state (left) and the goal state (right) for
the 24-puzzle.
The
24-puzzle is an extension of the 8-puzzle, where there are 24 pieces,
labeled with the numbers from 1 to 24, placed on a 5x5 grid. At each
move, a tile can move up, down, left, or right, but only if the
destination location is currently empty. For example, in the start
state shown above, there are three legal moves: the 12 can move down,
the 22 can move left, or the 19 can move right. The goal is to achieve
the goal state shown above. The cost of a solution is the number of
moves it takes to achieve that solution.
For
some initial states, the shortest solution is longer than 100 moves.
For all initial states, the shortest solution is at most 208 moves.
An
additional constraint is that, in any implementation, storing a search
node takes 1000 bytes, i.e., 1KB of memory.
Consider
general tree search using the stategies of
breadth-first search, depth-first search, iterative deepening search
and
uniform cost search.
(a):
Which (if any), among those methods, can guarantee that you will never
need more than 50KB of memory to store search nodes? Briefly justify
your answer.
(b):
Which (if any), among those methods, can guarantee that you will never
need more than 1200KB of memory to store search nodes? Briefly justify
your answer.




