Practice Questions and Answers

For each of the following agent environments, decide if it is fully or partially observable, deterministic or stochastic, static or dynamic, and discrete or continuous:
1. playing poker.
2. robot soccer player.
3. autonomous Mars rover.
4. playing tic-tac-toe.
5. mathematician's theorem-proving assistant.
Answer
1. playing poker: partially observable, stochastic, static, discrete.
2. robot soccer player: partially observable, stochastic, dynamic, continuous.
3. autonomous Mars rover: partially observable, stochastic, dynamic, continuous.
4. playing tic-tac-toe: fully observable, deterministic, static, discrete.
5. mathematician's theorem-proving assistant: fully observable, deterministic, static, discrete.
Suppose that an agent lives in a grid world of size 5 x 5 (for a total of 25 squares). The agent has two sensors: a GPS sensor, which informs the agent of its current location on the grid, and a camera sensor, which informs the agent of the color on the current square and the four adjacent squares. The agent, at each step, moves left, right, top, bottom. 24 of the 25 squares are safe, and one square (at location 4,3) is dangerous. The current location of the agent is safe.
a. If the agent is reflex-based, the safe squares are green, and the dangerous square is red, is it possible for this agent to follow a safe strategy that will always avoid the dangerous square? If yes, what is that strategy?

Answer
Yes, the strategy is to never visit a red square.
b. If the agent is reflex-based, and all squares (safe and dangerous) are green, is it possible for this agent to follow a safe strategy that will always avoid the dangerous square? If yes, what is that strategy?

Answer
Yes, the strategy is to never visit location (4,3), which can be achieved because the agent has a GPS sensor.
For the following tree, show the order of nodes visited for breadth-first search, depth-first search, uniform cost search, and iterative deepening search . The goal node is I and the numbers next to the edges indicate the associated cost.

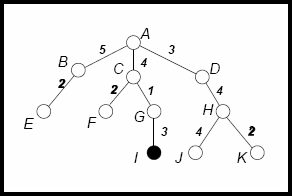
Answer
Note: in all methods, after goal node I is visited, the search stops. BFS: ABCDEFGHI
DFS: ABECFGI
UCS: ADCBGFEHI
IDS:
first iteration: A
second iteration: ABCD
third iteration: ABECFGDH
fourth iteration: ABECFGI
Does a finite state space always lead to a finite search tree? Justify your answer.
Answer
Yes if the algorithm remembers states already visited and thus avoids visiting each state an infinite number of times. No if the algorithm does not keep track of states already visited.
Textbook exercise 3.8, parts (a) and (b): Consider a state space where the start state is number 1 and the successor function for state n returns two states, numbers 2n and 2n+1.
a. Draw the portion of the state space for states 1 to 15.
Answer

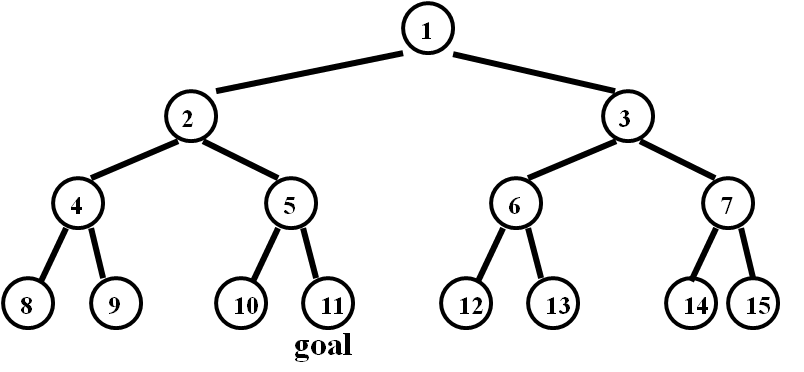
b. Suppose the goal state is 11. List the order in which nodes will be visited for breadth-first search, depth-limited search with limit 3, and iterative deepening search.

Answer
BFS: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
DLS (depth limit 3): 1, 2, 4, 5, 3, 6, 7

IDS:
first iteration: 1
second iteration: 1, 2, 3
third iteration: 1, 2, 4, 5, 3, 6, 7
fourth iteration: 1, 2, 4, 8, 9, 5, 10, 11
Describe a state space with 5 states, where the number of nodes visited by iterative deepening search (including the start node) is 15.
Answer
Quick answer: S1 -> S2 -> S3 -> S4 -> S5
More detailed answer:

States: S1, S2, S3, S4, S5.
Root: S1
Child of S1: S2
Child of S2: S3
Child of S3: S4
Child of S4: S5
Suppose that we are given a roadmap of the United States (i.e., we are given a list of roads, such that each road directly connects two cities). Additionally, we are given the distance from every city to Chicago. Consider the following heuristic (for possible use with A*): for each city A, h(A) = distance from A to Chicago + distance from Chicago to the goal. Is this heuristic admissible? Justify your answer.
Answer
No. If A is Dallas and the goal is Forth Worth, then h(A) > 1000 miles, which is clearly greater than the true distance from Dallas to Forth Worth.
An agent lives in a grid world of size 10 x 10. The goal of the agent is to find a rose. At every step, the agent can move left, right, up, or down. The agent has a sensor that detects the smell at the current square, and another sensor that detects if the current square contains a rose. Any square having distance 3 steps or less from a rose smells nicely, all other squares smell badly. Use this information to define a maximal admissible heuristic for this search problem (i.e., a heuristic that is not dominated by any other admissible heuristic that can be defined using this knowledge).
Answer
Heuristic h is defined as follows:
h(square) = 0 if the square smells nice.
h(square) = 4 if the square smells bad.

or

h(square) = 0 if the square smells nice and rose detected.
h(square) = 1 if the square smells nice and rose not detected.
h(square) = 4 if the square smells bad.
Perform minimax search with alpha-beta pruning for the following game tree. Indicate which nodes are never visited and which branches are pruned (assuming that ties are broken strictly from left to right ). Also indicate next to each node its computed value or an upper/lower bound for that value, as computed during the search.. The utilities of terminal nodes are indicated below the leaf nodes.

Answer
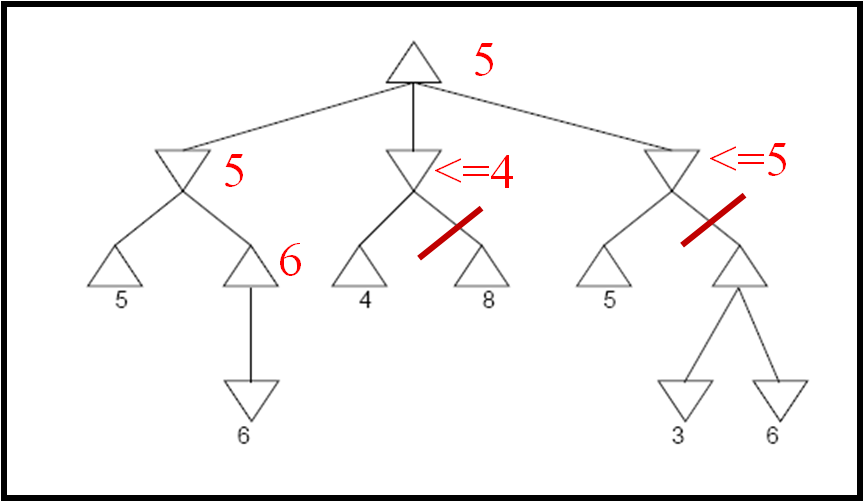
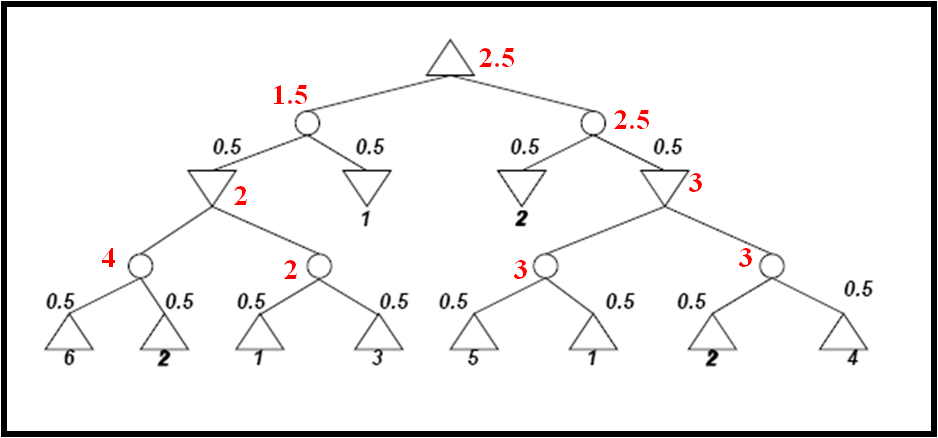
Determine the values of all nodes in the following game tree with chance nodes using Expectiminimax. The utilities of terminal nodes are indicated below the leaf nodes and the probabilities of chance nodes are next to the corresponding branches.

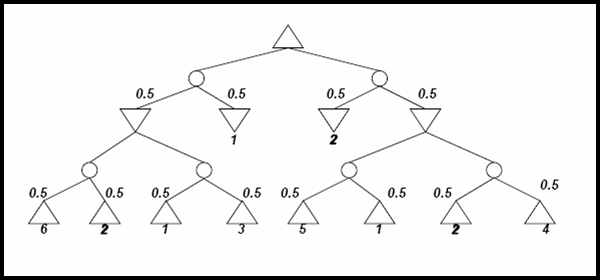
Answer