Assignment 2

Game Search & Constraint Satisfaction Problems

Problem 1

Max: [4308: 25 Points, 5360: 20 Points]

Draw the full Minmax tree for the game of TicTacToe starting from the given game state. Calculate the minmax value of every node and what the optimal action for the MAX player (X) to take is. (Note: Winning results in a payoff of +1 and losing a payoff of -1)


 O
 X
X
 X
 O
O


Figure 1: A TicTacToe Game State.


Problem 2

Max: [4308: 30 Points, 5360: 20 Points]

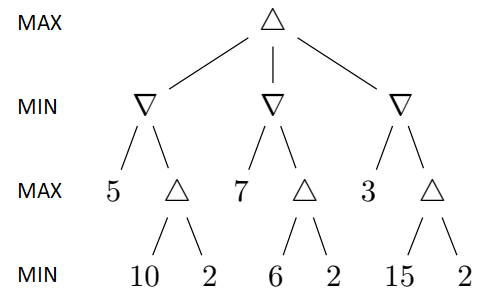
A Min Max Search Tree

Figure 2. A game search tree.

a. In the game search tree of Figure 2, indicate what nodes will be pruned using alpha-beta search, and what the mimax values are for the rest of the nodes. Assume that, when given a choice, alpha-beta search expands nodes in a left-to-right order. Also incidcate which action the Minmax algorithm will pick to exectute.

b. This question is also on the game search tree of Figure 2. Suppose we are given some additional knowledge about the game: the maximum utility value is 15 and the minimum utility is 2, i.e., it is not mathematically possible for the MAX player to get an outcome greater than 10 or lesser than -10. How can this knowledge be used to further improve the efficiency of alpha-beta search? Indicate the nodes that will be pruned using this improvement. Again, assume that, when given a choice, alpha-beta search expands nodes in a left-to-right order, and that the MAX player plays first.

c. If an agent uses this strategy against an optimal opponent what is the highest and lowest payoff it can get? What if it used this strategy against an opponent playing a random strategy?

Problem 3

Max: [4308: 20 Points, 5360: 20 Points]
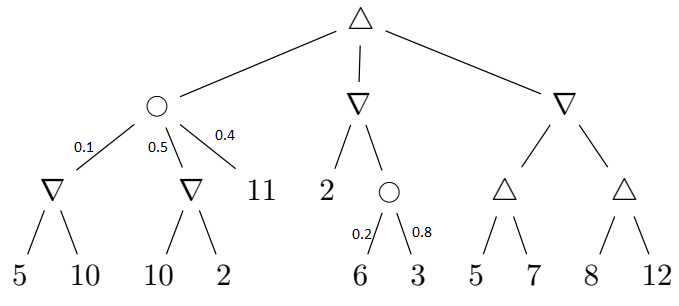
An Expectiminmax Tree
Figure 3. A expectiminmax tree.

 Find the value of every non-terminal node in the expectiminmax tree given above. Also indicate which action will be performed by the algoirithm.
What does the MinMax value obtained by the root node represent. For a particular game, what is the maximum and minmum actual payoff the MAX player can get if MIN plays the optimal strategy (according to Expectiminmax). What if the opponent plays a random strategy?

Problem 4

Max: [4308: 25 Points (+5 EC), 5360: 20 Points (+5 EC)]

The following outline map needs to be colored. The task is to color the various sections such that no two sections sharing a border have the same color. You are allowed to use the colors (Red, Green, Blue).

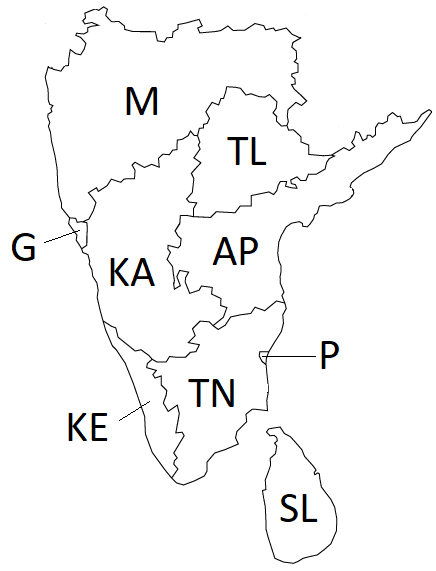
A Map of the Southern Part of the Indian Subcontinent
Figure 4. A map to be colored.

Part a: Draw the Constraint Graph for this problem. Can you use this information to simplify the problem?

Part b: Assuming you are using Backtracking search to solve the original version problem and that you are using both MRV and Degree heuristic to select the variable, Which variable will be selected at each level of the search tree [You do not need to draw the tree. Just let me know which variable will be selected and why (MRV and degree values)]. Note: Multiple possible answers. You only have to give one.

Part c: If we assign the color Red to the Variable at the first level of the backtracking search tree, show all the steps involved in checking arc consistency to find out the remaining legal values for the other variable

Part d: EC (5 points): Give one valid solution to this problem.

Problem 5 (Extra Credit for 4308, Required for 5360)

Max: [4308: 20 Points EC, 5360: 20 Points]

Suppose that you want to implement an algorithm tht will compete on a two-player deterministic game of perfect information. Your opponent is a supercomputer called DeepGreen. You do not know what algorithm DeepGreen uses. You are given a library function DeepGreenMove(S), that takes any state S as an argument, and returns the outcome of the move that DeepGreen will choose for that state S (more precisely, DeepGreenMove (S) returns the state resulting from the opponent's move).

Write an algorithm in pseudocode (following the style of the Minimax pseudocode) that will always make an optimal decision given the knowledge we have about DeepGreen. You are free to use the library function DeepGreenMove(S) in your pseudocode. How does this compare to Minimax wrt optimality of solution and the number of states explored.

How to submit

The assignment should be submitted via Canvas. Scan or Type the solutions for all the other Tasks together and create a single pdf titled assignment2_<net-id>.pdf. If multiple files are required zip them together into an archive titled assignment2_<net-id>.zip

Submission checklist

Is the file titled assignment1_<net-id>.pdf or assignment1_<net-id>.zip? (where <net-id> is replaced with your net id)
Did you upload the file on the submission page in Canvas and then click on 'Submit Assignment' to ensure that a submission is made?