Assignment 4

Written Assignment - Probablity & Bayesian Networks.

Max possible score:

4308: 85 Points
5360: 85 Points

Task 1 (20 Points)

Consider the given joint probabilty distribution for a domain of two variables (Color, Vehicle) :

	Color = Red	Color = Green	Color = Blue
Vehicle = Car	0.0450	0.0930	0.1620
Vehicle = Van	0.0495	0.1023	0.1782
Vehicle = Truck	0.0060	0.0124	0.0216
Vehicle = SUV	0.0495	0.1023	0.1782

Part a: Calculate P ( Color is not Green | Vehicle is Truck ) by Inference by Enumeration

Part b: Are Vehicle and Color totally independant from each other? Justify.

Task 2 (18 Points)

In a certain probability problem, we have 12 variables: A, B₁, B₂, ..., B₁₀, C.

Variable A has 8 possible values.
Each of variables B₁, ..., B₁₀ have 5 possible values. Each B_i is conditionally indepedent of all other 9 B_jvariables (with j != i) given A.
Variable C has 6 possible values. Variable C is totally independant of all other variables in the domain.

Based on these facts:

Part a: How many numbers do you need to store in the joint distribution table of these 12 variables?

Part b: What is the most space-efficient way (in terms of how many numbers you need to store) representation for the joint probability distribution of these 12 variables? How many numbers do you need to store in your solution?

Task 3 (10 Points)

George doesn't watch much TV in the evening, unless there is a baseball game on. When there is baseball on TV, George is very likely to watch. George has a cat that he feeds most evenings, although he forgets every now and then. He's much more likely to forget when he's watching TV. He's also very unlikely to feed the cat if he has run out of cat food (although sometimes he gives the cat some of his own food). Design a Bayesian network for modeling the relations between these four events:

baseball_game_on_TV
George_watches_TV
out_of_cat_food
George_feeds_cat

Your task is to connect these nodes with arrows pointing from causes to effects. No programming is needed for this part, just include an electronic document (PDF, Word file, or OpenOffice document) showing your Bayesian network design.

Task 4 (12 Points)

For the Bayesian network of previous task, the text file at this link contains training data from every evening of an entire year. Every line in this text file corresponds to an evening, and contains four numbers. Each number is a 0 or a 1. In more detail:

The first number is 0 if there is no baseball game on TV, and 1 if there is a baseball game on TV.
The second number is 0 if George does not watch TV, and 1 if George watches TV.
The third number is 0 if George is not out of cat food, and 1 if George is out of cat food.
The fourth number is 0 if George does not feed the cat, and 1 if George feeds the cat.

Based on the data in this file, determine the probability table for each node in the Bayesian network you have designed for Task 3. You need to include these four tables in the drawing that you produce for Task 5. You also need to submit the code/script that computes these probabilities.

Task 5 (10 Points)

Given the network obtained in the previous two tasks, calculate P ( not (Baseball Game on TV) | not(George Feeds Cat) ) using Inference by Enumeration

Task 6 (15 Points)

Figure 2: A Large Bayesian Network.

Part a: On the network shown in Figure 2, what is the Markov blanket of node N?

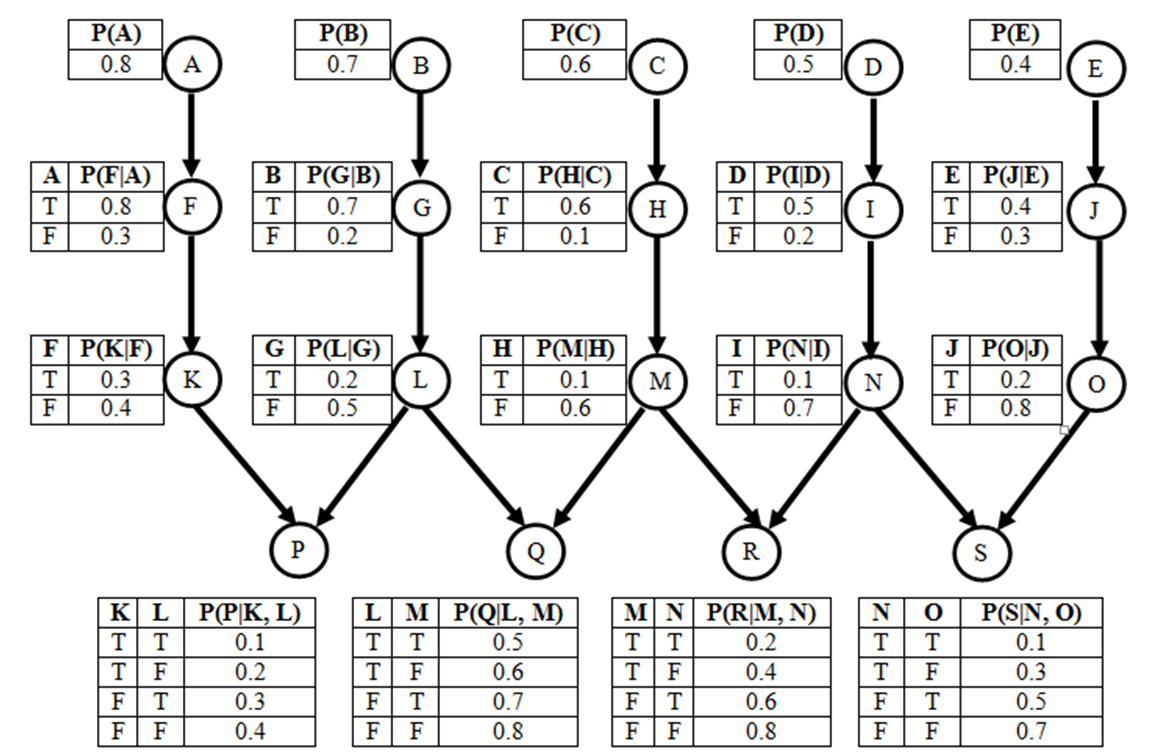
Part b: On the network shown in Figure 2, what is P(I, D)? (Note: You can use simplified calculations to calculate this as long as it is justified)

Part d: On the network shown in Figure 2, what is P(M, not(C) | H)? (Note: You can use simplified calculations to calculate this as long as it is justified)