Assignment 5

Written Assignment - Decision Trees, Bayesian Classifiers & Neural Networks.

Max possible score:

Task 1

20 Points

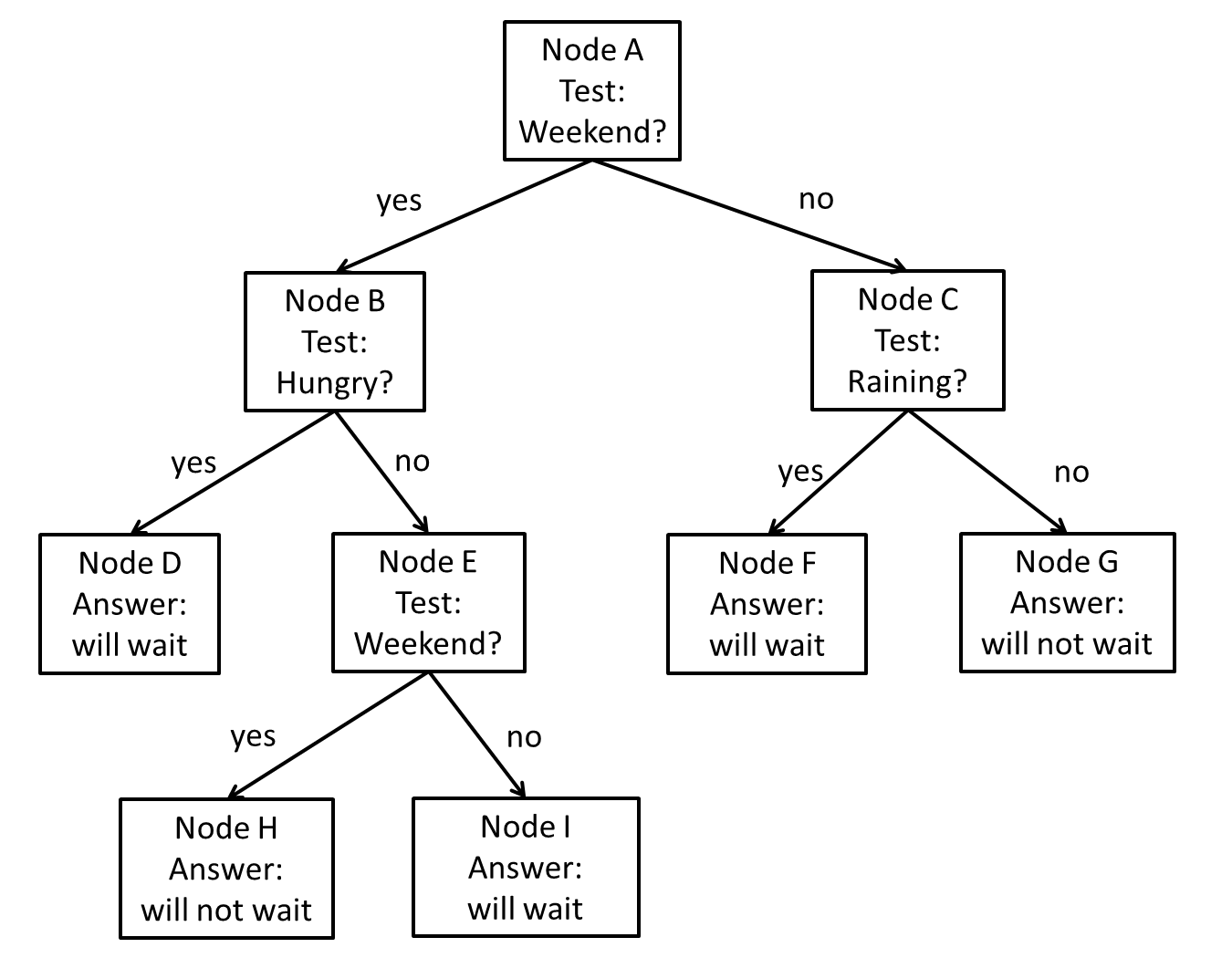
Decisiontree

Figure 1: A decision tree for estimating whether the patron will be willing to wait for a table at a restaurant.

Part a (5 points): Suppose that, on the entire set of training samples available for constructing the decision tree of Figure 1, 80 people decided to wait, and 20 people decided not to wait. What is the initial entropy at node A (before the test is applied)?

Part b (5 points): As mentioned in the previous part, at node A 80 people decided to wait, and 20 people decided not to wait.

What is the information gain for the weekend test at node A? 

Part c (5 points): In the decision tree of Figure 1, node E uses the exact same test (whether it is weekend or not) as node A. What is the information gain, at node E, of using the weekend test?

Part d (5 points): We have a test case of a hungry patron who came in on a rainy Sunday. Which leaf node does this test case end up in? What does the decision tree output for that case?

Task 2

15 points

  Class     A     B     C  
X 1 2 1
X 2 1 2
X 3 2 2
X 1 3 3
X 1 2 2
Y 2 1 1
Y 3 1 1
Y 2 2 2
Y 3 3 1
Y 2 1 1

We want to build a decision tree that determines whether a certain pattern is of type X or type Y. The decision tree can only use tests that are based on attributes A, B, and C. Each attribute has 3 possible values: 1, 2, 3. We have the 10 training examples, shown on the table (each row corresponds to a training example). What is the information gain of each attribute at the root? Which attribute achieves the highest information gain at the root?

Task 3

20 points

  Class     A     B     C  
X 25 24 31
X 22 14 24
X 28 22 25
X 24 13 30
X 26 20 24
Y 20 31 17
Y 18 32 14
Y 21 25 20
Y 13 32 15
Y 12 27 18

We want to build a decision tree (which thresholding) that determines whether a certain pattern is of type X or type Y. The decision tree can only use tests that are based on attributes A, B, and C. We have the 10 training examples, shown on the table (each row corresponds to a training example). Which attribute threshold combination achieves the highest information gain at the root? For each attribute try 5 thresholds evenly spaced between their lowest and highest values.

Task 4

20 points

Suppose that, at a node N of a decision tree, we have 1000 training examples. There are four possible class labels (A, B, C, D) for each of these training examples.

Part a: What is the highest possible and lowest possible entropy value at node N?

Part b: Suppose that, at node N, we choose an attribute K. What is the highest possible and lowest possible information gain for that accuracy?


Task 5

15 points

Consider the Training set for a Pattern Classification problem given below
Attribute 1 Attribute 2 Class
15 28 A
20 10 B
25 18 A
32 15 B
25 15 B
17 25 A

Assuming we want to build a Pseudo-Bayes classifier for this problem using one dimensional gaussians (with naive-bayes assumption) to approximate the required probabilties. Calculate the probabilites required.

Task 6

10 points

Can you design a single neuron that will return 1 if 4X - 7Y + 2Z = 6. If so give the weights of the neuron. If not, can you design a simple neural network to achieve the same result? If yes, give the weights of every node in that network.

Task 7 (EXTRA CREDIT)

5 points

Your boss at a software company gives you a binary bayesian classifier (i.e., a classifier with only two possible output values) that predicts, for any basketball game, whether the home team will win or not. This classifier has a 28% accuracy, and your boss assigns you the task of improving that classifier, so that you get an accuracy that is better than 60%. How do you achieve that task? Can you guarantee achieving better than 60%