Optional Assignment 2

Programming Assignment - Posterior Proabilites and Bayesian Networks

The assignment should be submitted via Canvas.

Sample output for the Tasks is given here.

Task 1 

50 points

The task in this part is to implement a system that: As in the slides that we saw in class, there are five types of bags of candies. Each bag has an infinite amount of candies. We have one of those bags, and we are picking candies out of it. We don't know what type of bag we have, so we want to figure out the probability of each type based on the candies that we have picked.

The five possible hypotheses for our bag are:

Command Line arguments:

The program takes a single command line argument, which is a string, for example CLLCCCLLL. This string represents a sequence of observations, i.e., a sequence of candies that we have already picked. Each character is C if we picked a cherry candy, and L if we picked a lime candy. Assuming that characters in the string are numbered starting with 1, the i-th character of the string corresponds to the i-th observation. The program should be invoked from the commandline as follows: 
compute_a_posteriori observations
For example: 
compute_a_posteriori CLLCCLLLCCL
We also allow the case of not having a command line argument at all, this represents the case where we have made no observations yet.

Output:

Your program should create a text file called "result.txt", that is formatted exactly as shown below. ??? is used where your program should print values that depend on its command line argument. Five decimal points should appear for any floating point number. 
Observation sequence Q: ???
Length of Q: ???

After Observation ??? = ???: (This and all remaining lines are repeated for every observation)

P(h1 | Q) = ???
P(h2 | Q) = ???
P(h3 | Q) = ???
P(h4 | Q) = ???
P(h5 | Q) = ???

Probability that the next candy we pick will be C, given Q: ???
Probability that the next candy we pick will be L, given Q: ???

Task 2 

50 points

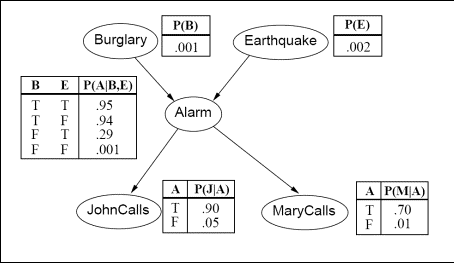
Earthquake_Burglary Net as discussed in Class

Figure 1: A Bayesian network establishing relations between events on the burglary-earthquake-alarm domain, together with complete specifications of all probability distributions.

For the Bayesian network of Figure 1, implement a program that computes and prints out the probability of any combination of events given any other combination of events. If the executable is called bnet, here are some example invocations of the program:

  1. To print out the probability P(Burglary=true and Alarm=false | MaryCalls=false). 
    bnet Bt Af given Mf
  2. To print out the probability P(Alarm=false and Earthquake=true). 
    bnet Af Et
  3. To print out the probability P(JohnCalls=true and Alarm=false | Burglary=true and Earthquake=false). 
    bnet Jt Af given Bt Ef
  4. To print out the probability P(Burglary=true and Alarm=false and MaryCalls=false and JohnCalls=true and Earthquake=true). 
    bnet Bt Af Mf Jt Et
In general, bnet takes 1 to 6(no more, no fewer) command line arguments, as follows: The implementation should not contain hardcoded values for all combinations of arguments. Instead, your code should use the tables shown on Figure 1 and the appropriate formulas to evaluate the probability of the specified event. It is OK to hardcode values from the tables on Figure 1 in your code, but it is not OK to hard code values for all possible command arguments, or probability values for all possible atomic events. More specifically, for full credit, the code should include and use a Bayesian network class. The class should include a member function called computeProbability(b, e, a, j, m), where each argument is a boolean, specifying if the corresponding event (burglary, earthquake, alarm, john-calls, mary-calls) is true or false. This function should return the joint probability of the five events.

Other Instructions