Assignment 3

Written Assignment - Game Playing & Logic

Max possible score:

4308: 150 Points
5360: 150 Points

Task 1

Max: [4308: 15 Points, 5360: 15 Points]

X		O
O		X
X	O

Figure 1. A tic-tac-toe board state.

Consider the tic-tac-toe board state shown in Figure 1. Draw the full minimax search tree starting from this state, and ending in terminal nodes. Show the utility value for each terminal and non-terminal node. Also show which move the Minimax algorithm decides to play for X. Utility values are +1 if X wins, 0 for a tie, and -1 if O wins. (Note: X is the MAX player).

Task 2

Max: [4308: 15 Points, 5360: 15 Points]

Note: This is a ABET Assesment Task

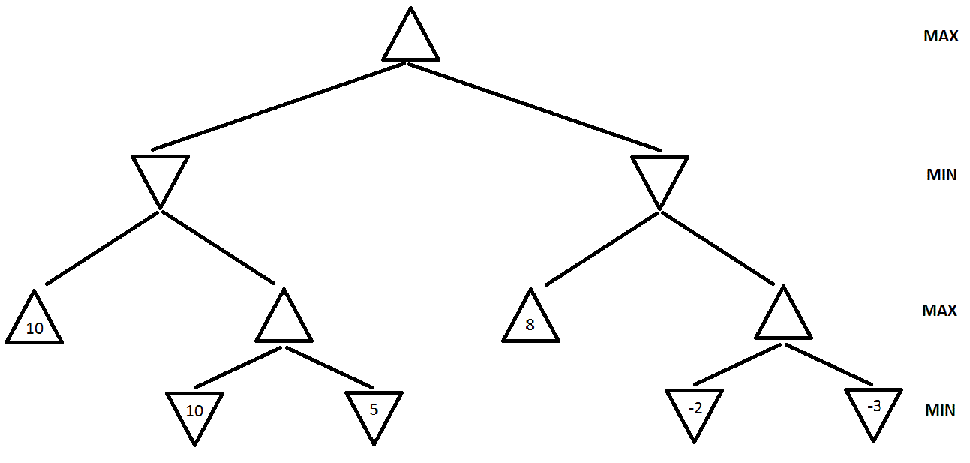
MinmaxTree

Figure 2. A game search tree.

a. (4308: 10 points, 5360: 10 points) In the game search tree of Figure 2, indicate what nodes will be pruned using alpha-beta search, and what the estimated utility values are for the rest of the nodes. Assume that, when given a choice, alpha-beta search expands nodes in a left-to-right order. Also, assume the MAX player plays first. Finally incidcate which action the Minmax algorithm will pick to exectute.

b. (4308: 5 points, 5360: 5 points) This question is also on the game search tree of Figure 2. Suppose we are given some additional knowledge about the game: the maximum utility value is 10, i.e., it is not mathematically possible for the MAX player to get an outcome greater than 10. How can this knowledge be used to further improve the efficiency of alpha-beta search? Indicate the nodes that will be pruned using this improvement. Again, assume that, when given a choice, alpha-beta search expands nodes in a left-to-right order, and that the MAX player plays first.

Task 3

Max: [4308: 10 Points, 5360: 10 Points]

Suppose that you want to implement an algorithm that will compete on a two-player deterministic game of perfect information. Your opponent is a supercomputer called DeepGreen. DeepGreen does not use Minimax. You are given a library function DeepGreenMove(S), that takes any state S as an argument, and returns the move that DeepGreen will choose for that state S (more precisely, DeepGreenMove (S) returns the state resulting from the opponent's move).

Write an algorithm in pseudocode (following the style of the Minimax pseudocode) that will always make an optimal decision given the knowledge we have about DeepGreen. You are free to use the library function DeepGreenMove(S) in your pseudocode. What advantage would this algorithm have over Minimax? (if none, Justify).

Task 4

Max: [4308: 10 Points, 5360: 10 Points]

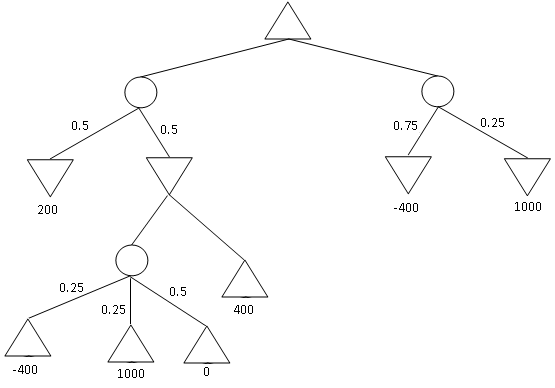
Figure 3: An Expectiminmax tree.

Find the value of every non-terminal node in the expectiminmax tree given above. Also indicate which action will be performed by the algoirithm. What is lowest and highest possible outcome of a single game if the minmax strategy is followed.

Task 5

Max: [4308: 10 Points, 5360: 10 Points]

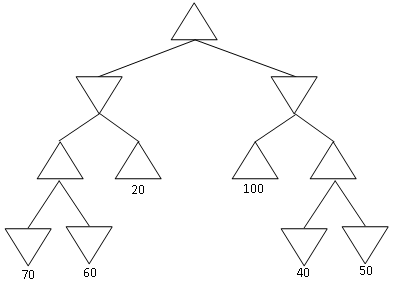
Figure 4: Yet another game search tree

Consider the MINIMAX tree above. Suppose that we are the MAX player, and we follow the MINIMAX algorithm to play a full game against an opponent. However, we do not know what algorithm the opponent uses.

Under these conditions, what is the best possible outcome of playing the full game for the MAX player? What is the worst possible outcome for the MAX player? Justify your answer.

NOTE: the question is not asking you about what MINIMAX will compute for the start node. It is asking you what is the best and worst outcome of a complete game under the assumptions stated above.

Task 6

Max: [4308: 10 Points, 5360: 10 Points]

Two logical statements S1 and S2 are logically equivalent if (S1 <=> S2) is valid. We have two knowledge bases, KB1 and KB2.. Write a function CHECK_EQUIVALENCE(KB1, KB2) that:

returns true if KB1 and KB2 are logically equivalent.
returns false otherwise.

Your pseudocode can re-use any code from the textbook or slides, and can call any of the functions given in the textbook or slides, as long as such code and functions are used correctly, with correct names for the functions, and with well-specified values for all variables and arguments.

Task 7

Max: [4308: 10 Points, 5360: 10 Points]

A	B	C	KB	S1
True	True	True	True	True
True	True	False	False	True
True	False	True	True	True
True	False	False	False	True
False	True	True	False	False
False	True	False	False	False
False	False	True	True	True
False	False	False	False	False

KB and S1 are two propositional logic statements, that are constructed using symbols A, B, C, and using various connectives. The above truth table shows, for each combination of values of A, B, C, whether KB and S1 are true or false.

Part a: Given the above information, does KB entail S1? Justify your answer.

Part b: Given the above information, does statement NOT(KB) entail statement NOT(S1)? Justify your answer.

Task 8

Max: [4308: 10 Points, 5360: 10 Points]

Suppose that some knowledge base contains various propositional-logic sentences that utilize symbols A, B, C, D (connected with various connectives). There are only two cases when the knowledge base is false:
- First case: when A is true, B is false, C is true, D is true.
- Second case: when A is false, B is false, C is true, D is false.

In all other cases, the knowledge base is true. Write a conjunctive normal form (CNF) for the knowledge base.

Task 9

Max: [4308: 20 Points, 5360: 20 Points]

Note: This is a ABET Assesment Task

Consider the KB

A => B
B <=> C
D => A
E => D
C AND E => F
E

Show that this entails F by

i. Forward Chaining
ii. Backward Chaining
iii. Resolution

Task 10

Max: [4308: 40 Points, 5360: 40 Points]

In April, John and Mary sign the following contract:

- If it rains in May, then John must give Mary a check for $10,000
- If John gives Mary a check for $10,000, Mary must mow the lawn.

What truly happened those days is the following:
- It did not rain in May.
- John gave Mary a check for $10,000
- Mary mowed the lawn.

Part a: Write a first order logic statement to express the contract. Make sure that you clearly define what constants and predicates that you use are. (NOTE: DO NOT use functions)

Part b: Write a logical statement to express what truly happened. When possible, use the same predicates and constants as in question 6a. If you need to define any new predicates or constants, clearly define what they stand for.

Part c: Define the symbols required to convert any KB involved in the above domanin from FOL to Propositional logic (Your symbols must allow me to convert ANY KB that uses the predicates and constants as decribed previously).

Part d: Use the sybols given in part c, to convert the answers to part a and b to Propositional Logic.

Part e: Was the contract violated or not, Justify your answer (Note: if the sequence of events that occured entails the contract then it was not violated)